|
Question 135117: May you please help me with this Problem?
the directions say Factor each polynomial if possible. If the polynomial cannot be factored write prime.
a^2-14+36
And another Question how do you know if the polynomial is prime or not?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! First thing is that I think you made an error when you wrote your polynomial. It probably should be 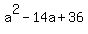 . .
Presuming that, a little discussion is in order. In the first place, all second degree polynomials are factorable as long as you aren't too restrictive about the numbers that you use as factors. Since your instructor is using the term "prime" I'm going to assume that you meant that you wanted to factor the polynomial over the rational numbers (those numbers that can be represented as the ratio of two integers).
The first step is to look at the signs on the 1st degree and constant terms. The sign on the constant term is positive and that tells us that the signs on the factors must be the same. The sign on the 1st degree term is negative and that tells us that the signs of both terms must be negative.
(If the constant term sign was negative, then the signs of the factors must be different. In this case, if the 1st degree term is negative, the larger of the two factors must be negative)
Second step is to find all the prime factors of the constant term, that is the 36.
2 * 2 * 3 * 3 = 36.
Now we can investigate all of the possible pairs of integers that have a product of 36.
1 * 36
2 * 18
4 * 9
6 * 6
Now go back and add these pairs of numbers
1 + 36 = 37
2 + 18 = 20
4 + 9 = 13
6 + 6 = 12
None of the pairs add up to 14, therefore there are no rational factors. You would call this trinomial "prime"
If you were working with a trinomial with a negative sign on the constant term, then, instead of adding the numbers as we did above, you would subtract them. Since the factors have different signs, you need to find the difference that is equal to the coefficient on the 1st degree term.
Just because you can't find rational factors however doesn't mean there aren't any.

|
|
|
| |