Question 134896: If I have to Let ABC have vertices a(-6,3),B(-1,-4), and C(3,-5).Give the coordinates of the vertices of the image after the specified transformation.
18. 180 degree rotation
How does that work? Any help with this equation would be appreciated.:)
Found 2 solutions by scott8148, solver91311:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! rotation means the point (vertex) is moving around a circle that is centered at the origin (0,0)
180° is halfway around the circle __ remember that positive degrees are counterclockwise
operationally, a 180° rotation is like a reflection through the origin
__ the x and y numbers stay the same, but the signs change
new vertices __ A(6,-3), B(1,4), C(-3,5)
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Convert each of the points to polar coordinates by using the formulas:
 for for  and and 
 for for  and and 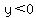
 for for 
 for any of your given points so we can ignore those cases for any of your given points so we can ignore those cases

Once you have converted all three points to polar coordinate ( , , ) form, substitute ) form, substitute  for the for the  in each of the points. Since in each of the points. Since  radians equals 180 degrees, this has the effect of applying the 180 degree rotation transformation. radians equals 180 degrees, this has the effect of applying the 180 degree rotation transformation.
Finally, convert the new polar coordinates back to rectangular coordinates by use of the formulas:


I'll do one of the points and you can finish up.
A(-6,3). Here,  , so we need , so we need 

 approx 2.678, but we'll leave it in terms of arctan for the moment because we are just going to convert back anyway. approx 2.678, but we'll leave it in terms of arctan for the moment because we are just going to convert back anyway.

so the polar representation of the cartesian point (-6,3) is (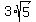 , ,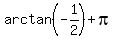 ) )
Now, to rotate this point 180 degrees, add  to the angle, and the new polar point is ( to the angle, and the new polar point is (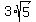 , ,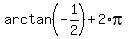 ) )
Converting back to rectangular,


Actually, the answer makes very good sense if you try an experiment. Plot your points on a piece of graph paper, then turn the paper upside down -- in other words, rotate the page 180 degrees. If you then change all of the signs on the scale numbers, you will see that you have the coordiates of the transformed points.
|
|
|