SOLUTION: I am completely lost on how to do these. Any help would be great. It says: Sketch the graph of the following. Label vertex, x-and y-intercepts. f(x)=x^2-x-12 Vertex=( , ) x-

Algebra ->  Coordinate-system -> SOLUTION: I am completely lost on how to do these. Any help would be great. It says: Sketch the graph of the following. Label vertex, x-and y-intercepts. f(x)=x^2-x-12 Vertex=( , ) x-      Log On


   

Question 134725This question is from textbook College Algebra
: I am completely lost on how to do these. Any help would be great.
It says:
Sketch the graph of the following. Label vertex, x-and y-intercepts.
f(x)=x^2-x-12
Vertex=( , )
x-intercepts=( , );( , )
y-intercept=( , ) This question is from textbook College Algebra

Found 3 solutions by cbcrawford978, ankor@dixie-net.com, solver91311:
Answer by cbcrawford978(7) About Me  (Show Source):
You can put this solution on YOUR website!
The easiest way to solve this is on a graph. But i'm going to factor the equation to find ONLY the x-intercepts.....x%5E2-x-12 This factors into x-4=0 and x%2B3=0 if you use the FOIL method %28x-4%29%28x-3%29 you should get x%5E2-x-12. The reason you set x-4 and x%2B3 to "0" is so you can solve for "x." x-4=0.....x=4 and x+3=0......x=-3. The x-intercepts are (4,0) and (-3,0). You should make a graph to find the y-intercept. Since the highest power in the equation is "2" there should only be one y-intercept. The vertex is the lowest point on the graph.graph%28300%2C200%2C-5%2C5%2C-15%2C15%2Cx%5E2-x-12%29

Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
I am completely lost on how to do these. Any help would be great.
It says:
Sketch the graph of the following. Label vertex, x-and y-intercepts.
f(x) = x^2 - x - 12
Here's how you can sketch a graph
f(x) = y so we have:
y = x^2 - x - 12
:
We will find the values of y by substituting -5 to +5 in the equation
A table of these value will be:
x | y
-------
-5 |+18
-4 |+8
-3 |0; when y = 0, this is one of the x intercepts
-2 |-6
-1 |-10
0 |-12; notice when x = 0, the value of y is 12, this is the y intercept
+1 |-12; it has reached a minimum and started back up again
+2 |-10
+3 |-6
+4 | 0; this is the 2nd x intercept
+5 |+8
Plot these values, it should look like this:
+graph%28+300%2C+200%2C+-10%2C+10%2C+-16%2C+10%2C+x%5E2-x-12%29+
:
Vertex=( , )
To find the vertex, first find the axis of symmetry. This can be found using the formula x = -b/(2a)
In this equation a=1; b=-1
x = 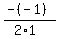%28-%28-1%29%29%2F%282%2A1%29
x = 1%2F2 or .5
Find the vertex by substituting 1/2 for x in the original equation:
y = .5^2 - .5 - 12
y= .25 - .5 - 12
y = -12.25
The x/y values for the vertex is: .5, -12.25, this is the minimum as you can see by the graph
:
x-intercepts=( , );( ,
x intercepts are the points which the graph crosses the x axis (y=0)
you can find them by solving the equation
x^2 - x - 12 = 0
Factors to
(x-4)(x+3) = 0
x = +4
x = -3; the x intercepts
:
y-intercept=( , )
As we said the y intercept occurs when x = 0, you see when substitute 0 for x in the equation; y = -12
:
Did this help you? Do you have any questions?

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Your function is in the form f%28x%29=ax%5E2%2Bbx%2Bc where a=1, b=-1, and c=-12

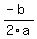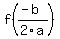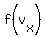The vertex is located at the point (%28-b%29%2F2a,f%28%28-b%29%2F2a%29). So, calculate v%5Bx%5D=%28-b%29%2F2a to get the x-coordinate, then evaluate f%28v%5Bx%5D%29 to get the y-coordinate. Plot this point on your graph.

The x-intercepts are at (p,0) and (q,0) where x=p and x=q are the solutions to f(x)=0. So solve +x%5E2+-+x+-+12+=+0 to determine p and q, then plot these two points.

The y-intercept is at (0,f(0)). Evaluate f(0) by substituting 0 for x in x%5E2-x-12. Plot this point.

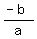Multiply the x-coordinate of the vertex by 2. Symmetry of the curve about the vertical line x+=+%28-b%29%2F2a means that there will be another point on the curve at (%28-b%29%2Fa,f%280%29), i.e. 2 times the x-coordinate of the vertex and the y-coordinate of the y-intercept. Plot this point.

Draw a smooth curve through the plotted points. Done.

It should look something like this: