Question 134542This question is from textbook
: 2log base3(x+4)=log base 3 9+2
solve for x
This question is from textbook
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You either meant: 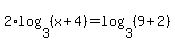 or or 
Let's assume you meant the first one:
 , so: , so:

=> 
 or or 
and finally, 
However, since  , , 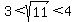 . That means that . That means that 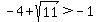 and and 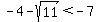 . .
The domain of 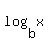 is is 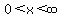 , so the domain of , so the domain of  must be must be 
Therefore, 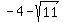 must be excluded since it represents a value that would make must be excluded since it represents a value that would make  be outside of the domain of be outside of the domain of  . .
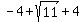 is in the domain of is in the domain of  , therefore , therefore  completely describes the solution set for the given equation. completely describes the solution set for the given equation.
On the other hand, if you really meant:

Then begin with the same rule for logarithms used above, namely:  to write: to write:

Since  if and only if if and only if  , we can say , we can say  if and only if if and only if  and therefore and therefore  , hence: , hence:

Again using  if and only if if and only if  , we can write: , we can write:

Taking the square root of both sides:
 or or 
And
 or or  . Using the same logic as above, exclude any root less than -4. . Using the same logic as above, exclude any root less than -4.  is the single element of the solution set. is the single element of the solution set.
|
|
|