Question 134381: Find the smallest whole number that when divided by 5,7,9, and 11, respectively, gives remainders of 1,2,3, and 4.
Answer by vleith(2983)   (Show Source):
You can put this solution on YOUR website! Not sure if this is correct, but gie it a look and see what you think
Step 1. Find a number that fits for 5 and 7
The smallest number that fits for 5 is 6
So, we need to find a number such that:
(6 + 5x)/7 has a remainder of 3
Using Modulo arithmetic:
6 modulo 7 = 6
We need to find a value for (5x)Modulo 7 that equals 3 (so the sums of of the remainders of two parts on the left would be 6 + 4 = 10 = 3 Modulo 7
If we take x =1, then 5/7 = 5. which is not 4
If we take x =2, the 10/7 = 3. Which is what we want. so the smallest number for 5 and 7 = 6 + 5(2) = 16.
Next we want to add in 9.
Again, we start with the smallest number that fits both 5 and 7. This time the multiple is (5*7)
So the list series of numbers that fit 5/7/9 is
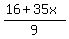
Again using modulo approach, we want the remainder to = 3
16Mod9 = 7. So the second term must have a remainder of 5 in order for the entire sum to have a remainder of 3 (7 + 5) = 12 = 3Modulo 9
x = 1, yields remainder 0
x = 2 yields 7
x = 3 yields 6
x = 4 yields 5 which is what we want
So, the smallest number that works for 5/7/9 is 16+35(4) = 156
Now we do the same thing for the 11
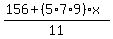 is to yiled a remainder of 4
156Mod11 = 2, so the second term needs to leave a remainder of 2 for a total of 4
315x/11
x = 1 yeilds 7
x = 2 yields 3
x = 3 yields 10
x = 4 yields 6
x = 5 yields 2 which is what we want (notice the remainders decrease by 4 each time)
So the number we want is 156 + 315(5) = 1731
That works for the all the reamainders. Now verify it is the smallest number that works.
Factor 1731 into it's primes. that yields 3 and 577
The number cannot include any factors of 5,7,9 or 11. I tried using trial and error to get a smaller number, but can;t. So I think 1731 is correct
|
|
|
