(I'll use Q instead of @, so my computer won't think it's
an email address. Igor hasn't put in the Greek letter "theta"
in his program. Think I'll ask him to put it in.)
-------------------------------------------------------
Given that cosQ =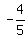 
and Q is in Quadrant 2, find:
-------------------------------------------------------
Draw the picture of Q. We use the numerator and denominator
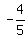of for x and r. Since 
, to put
q in Quadrant 2, we must take x as 
and 
as 
,
and draw this picture, with the curved line indicating angle Q:
Now we use the Pythagorean theorm to find 
±
±
But since goes upward from the x-axis,
we take the positive value, so 
-------------------------------------
To find
sinQ, we only need to know that sinQ = 
or 
-------------------------------------
To find
sin2Q, we need the identity sin2A = 2sinAcosA
sin2Q = 2sinQcosQ
sin2Q = 2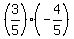
sin2Q = 
--------------------------------------------
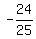To find
cos3Q, we need the identities cos(A+B) = cosAcosB - sinAsinB and cos2A = 2cos²A-1
First we rewrite 3Q as 2Q+Q
Then by the first identity,
cos3Q = cos(2Q+Q) = cos2QcosQ - sin2QsinQ
= cos2Q(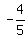) - sin2Q()
and we have already found sin2Q to be ,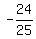
so
= cos2Q() - (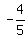
)
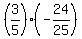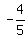= ()cos2Q - (
)
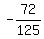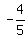= cos2Q + 
Now we use the second identity to rewrite cos2Q
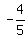= (2cos²Q - 1) +
Distribute:
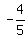= (2cos²Q) + 
+
= 
cos²Q + +
Combine the last two terms and substitute 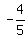for cosQ
= 
+ 
=
= 
+
= 
+
= 
---------------------------------------
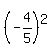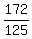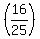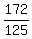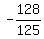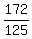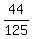To find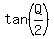 
, we use the identity 
= 
= 
= 
= 
= 
= 
= 
= 
= 
----------------
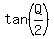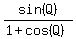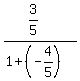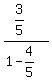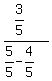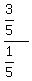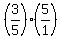To find sin(Q + 60°) we use identity sin(A + B) = sinAcosB + cosAsinB
sin(Q + 60°) = sinQcos60° + cosQsin60°
Now we use the fact that cos60° = 
, sin60° = 
, cosQ = 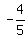and sinQ =
sin(Q + 60°) = 
=
=
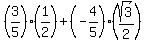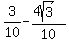Edwin
