Question 134104: How can you simplify radicals?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Perform a prime factorization of the quantity under the radical. If any of the prime factors occur in pairs, remove the pair from under the radical and put a single instance of the factor outside the radical. Once all the pairs have been removed, re-combine the remaining factors under the radical, and combine any factors you have moved outside of the radical.
Example: 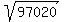
97020/2 = 48510 One factor of 2, still even
48510/2 = 24255 Another factor of 2, no longer even, but sum of digits div by 3
24255/3 = 8085 One factor of 3, sum of digits still div by 3
8085/3 = 2695 Another factor of 3, sum of digits not div by 3, but ends in 5
2695/5 = 539 One factor of 5, Does not end in 5, so try 7
539/7 = 77 One factor of 7
77/7 = 11 Another factor of 7
11 Is prime.
Factors: 2 * 2 * 3 * 3 * 5 * 7 * 7 * 11.
Pair of 2s, pair of 3s, and pair of 7s, so
 . And that is as simple as you can make it. . And that is as simple as you can make it.
Example 2:
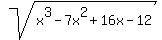
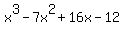 divided by divided by  = =  (use synthetic division to verify this for yourself). And (use synthetic division to verify this for yourself). And  factors to factors to 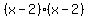 , so: , so:

|
|
|