Question 134042: #1) three times the width of a certain rectangle exceeds twice its lenght by three inches, and four times its length is twelve more than its perimeter. Find the dimensions of the rectangle.
#2) The larger of the 2 intergers is 5/2 the smaller. If twice the smaller is subtracted from twice the larger, the difference is 12. Find the two numbers.
#3) The tens digit of a two digit number is two more than the ones digit. The number is thirty more than four times the sum of the digit. What is the number?
could u please solve thesse problems give your equations and an explanation of how you got it.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! These are all really the same sort of problems, so I'll do one of them.
Width of a rectangle: W
Three times the width: 3W
Length of a rectangle: L
Twice the length: 2L
Three inches more than twice the length: 2L + 3
So: 3W = 2L + 3
The perimeter of a rectangle: P = 2L + 2W, so the perimeter plus 12 would be 2L + 2W + 12, and that is equal to four times the length, or 4L, so:
4L = 2L + 2W + 12
Take the first equation and solve for W: 
Substitute this expression for W into the second equation:

Multiply both sides by 3:

Distribute:

Collect terms:


Divide:

Since 

For the other two problems, define your variables, set up the given relationships, solve one of them for one variable in terms of the other, substitute, and finally solve for one of the variables.
Hint for the second problem: Let x be the smaller integer, and then the larger integer is 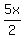 . .
Hint for the third problem: If x and y are the tens and ones digits of a number, the number is 10x + y and the sum of the digits is x + y.
|
|
|