Question 133976This question is from textbook
: What are the leading coefficient, the polynomial by degree and by the number of terms?
This question is from textbook
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, terms are the parts of the polynomial separated by + and - signs:
 has three terms, namely has three terms, namely  , , 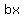 , and , and 
The degree of a polynomial is the highest exponent on any term in the polynomial, so  is a polynomial of degree 2. But be careful, this can be tricky to determine if there are multiple variables. For example, is a polynomial of degree 2. But be careful, this can be tricky to determine if there are multiple variables. For example,
 is a polynomial of degree 4. That is because you must add the exponents on all variables in any given term. is a polynomial of degree 4. That is because you must add the exponents on all variables in any given term.
 is a term of degree 2 is a term of degree 2
 is a term of degree 3, because if there is no exponent on a variable the exponent is understood to be 1. The exponent on x is 1 and the exponent on y is 2, so the degree is 1 + 2 = 3. is a term of degree 3, because if there is no exponent on a variable the exponent is understood to be 1. The exponent on x is 1 and the exponent on y is 2, so the degree is 1 + 2 = 3.
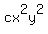 is a term of degree 4 -- 2 + 2 = 4. is a term of degree 4 -- 2 + 2 = 4.
 is a term of degree 1 is a term of degree 1
Since the highest degree term has a degree of 4, the whole polynomial is degree 4.
Coefficients are the 'number' part of the term as opposed to the variable part. So if you have 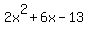 , the coefficients are 2, 6, and -13. Always remember that a minus sign is part of the coefficient. When we talk about general forms of a polynomial, such as the general quadratic: , the coefficients are 2, 6, and -13. Always remember that a minus sign is part of the coefficient. When we talk about general forms of a polynomial, such as the general quadratic:  we use general terms for the coefficients. Here the coefficients are a, b, and c. we use general terms for the coefficients. Here the coefficients are a, b, and c.
When a polynomial is written in standard form, the terms are written in decending order of degree, meaning the highest degree term is first, and the next highest degree term is second, and so on. When this is done, the coefficient on the first term is referred to as the lead coefficient. So in  , a is the lead coefficient. , a is the lead coefficient.
|
|
|