SOLUTION: Find the vertex and intercepts for the parabola g(x)=x^2+x-6 Sketch the graph

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Find the vertex and intercepts for the parabola g(x)=x^2+x-6 Sketch the graph      Log On


   

Question 133461: Find the vertex and intercepts for the parabola g(x)=x^2+x-6 Sketch the graph
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
The vertex of a parabola in the form 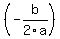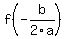f%28x%29=ax%5E2%2Bbx%2Bc is located at the point (%28-b%2F2a%29,f%28-b%2F2a%29)

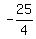For your g%28x%29=x%5E2%2Bx-6, a=1, b=1, and c=-6, so the x-coordinate of the vertex is -1%2F2%281%29=-1%2F2, and the y-coordinate of the vertex is g%28-1%2F2%29=%28-1%2F2%29%5E2%2B%28-1%2F2%29-6=1%2F4-1%2F2-6=-25%2F4, so you can say that the vertex is located at: (1%2F2,-25%2F4%29)

The intercepts are where g%28x%29=0, so solve x%5E2%2Bx-6=0.

Factor:
%28x-2%29%28x%2B3%29=0

x=2 or x=-3 => intercepts at (2,0) and (-3,0)