Question 133213: Find the equation of the line through the given pair of points in standard form using only integers?
(-4,-1) and (5,8)
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: Start with the slope formula (note: ) is the first point ( is the first point ( , , ) and ) and ) is the second point ( is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 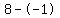 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 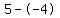 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and is the slope, and ) is one of the given points is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite  as as 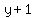
 Rewrite Rewrite 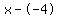 as as 
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
|
|