Question 132970: Can you explain me how do I find the asymptotes of the functions f(x)=3^x and
g(x) = log5(2x).
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! 
First,  is not an asymptote because 
and  .  changes smoothly on either side of
 and  , so the plot is
. . 
.989 . . -0.01
1 . . 0
1.011 . . 0.01
The smooth changes in both and means there is
no asyptote
-------------
As becomes infinitely large in the + direction,
becomes larger at an even greater rate without any bounds.
As becomes larger in the negative direction, however,
gets closer and closer to  , but never
becomes negative. There is no way 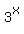 can possibly be negative.
is the definition of the x-axis, so the negative
x-axis is an asyptote
--------------------------
g(x) = log5(2x)
If I say  , I can rewrite the equation as
Is an asymptote? If ,  approaches
negative infinity. There is no way that  can ever be
negative since 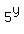 can never be negative. is the
definition of the y-axis, so the y-axis is an asymptote
When becomes very large in the + direction,
also becomes very large, just not at as fast a rate.
I'll plot the curves
|
|
|
