|
Question 132820: Pleeease HELP
I have read and reread the text and can not answer this question at all
Solve the compound inequality. Write the solution set using interval notation and graph it.
-7x+1 (greater than or equal to sign)15 or 5x + 3 (greater than or equal to sign) -17
I don't know where to begin-any suggestions would be appreciated-Thank You
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! You have two inequalities joined by the word 'or':
 or 
The meaning of 'or' is 'one or the other, and maybe both' So we need to find those values of x that will make either the first inequality true or the second one true.
The first step is to solve each of the inequalities for x:
Add -1 to both sides:
Divide both sides by -7. Here is where solving an inequality differs from solving an equation. When solving an equation, you can multiply or divide both sides by anything you want and still maintain the equal relationship, but if you multiply or divide an inequality by a negative number, the sense of the inequality changes. Here's a trivial example that illustrates what I mean:
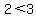 is certainly a true statement. But if you multiply by -1, you get -2 on one side and -3 on the other, but that means that you have to turn the inequality sign around to keep it a true statement since clearly  .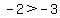
=================
Add -3 to both sides:
Divide by 5. This time we don't have to change the sense of the inequality because we are dividing by a positive number, namely 5.
Every real number is less than -2 OR greater than -4, so the solution set to the given system of inequalities is all real numbers. In interval notation: ( , ).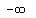
Note that had the connective been AND rather than OR, the solution set would have been all values that are both greater than or equal to -4 AND less than or equal to -2, and the interval would be denoted [-4,-2]. The square brackets in interval notation mean that the endpoints are included, and they are included in this example because of the 'or equal' part of each of the inequalities. As an aside, the 'maybe both' part of the definition I gave for the word 'or' is this very interval.
|
|
|
| |
