SOLUTION: {{{ 3/(x-2) + 5/(x+2) = 4x^2/(x^2-4) }}} I am trying to solve this problem however I do not even know how to begin to work it out. How do I solve this problem?

Algebra ->  Rational-functions -> SOLUTION: {{{ 3/(x-2) + 5/(x+2) = 4x^2/(x^2-4) }}} I am trying to solve this problem however I do not even know how to begin to work it out. How do I solve this problem?      Log On


   

Question 132602This question is from textbook Algebra II
: +3%2F%28x-2%29+%2B+5%2F%28x%2B2%29+=+4x%5E2%2F%28x%5E2-4%29+
I am trying to solve this problem however I do not even know how to begin to work it out. How do I solve this problem? This question is from textbook Algebra II

Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
+3%2F%28x-2%29+%2B+5%2F%28x%2B2%29+=+4x%5E2%2F%28x%5E2-4%29+ Start with the given equation


+3%2F%28x-2%29+%2B+5%2F%28x%2B2%29+=+4x%5E2%2F%28%28x-2%29%28x%2B2%29%29+ Factor x%5E2-4 to get %28x-2%29%28x%2B2%29


Notice how the LCD is %28x-2%29%28x%2B2%29



Multiply both sides by the LCD %28x-2%29%28x%2B2%29. Doing this will eliminate every fraction.


3%28x%2B2%29%2B5%28x-2%29=4x%5E2 Distribute and multiply. Notice every denominator has been canceled out.


3x%2B6%2B5x-10=4x%5E2 Distribute again


8x-4=4x%5E2 Combine like terms


8x-4-4x%5E2=0 Subtract 4x%5E2 from both sides.


-4x%5E2%2B8x-4=0 Rearrange the terms


-4%28x-1%29%28x-1%29=0 Factor the left side (note: if you need help with factoring, check out this solver)



Now set each factor equal to zero:
x-1=0 or x-1=0

x=1 or x=1 Now solve for x in each case


Since we have a repeating answer, our only answer is x=1


---------------------------------------------------------------------

Answer:

So the solution is x=1

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
+3%2F%28x-2%29+%2B+5%2F%28x%2B2%29+=+4x%5E2%2F%28x%5E2-4%29+

The first step is to recognize that x%5E2-4 is the difference of two squares that factors thusly: a%5E2-b%5E2=%28a%2Bb%29%28a-b%29. So, x%5E2-4=%28x%2B2%29%28x-2%29. That means that you can re-write your equation like this:

+3%2F%28x-2%29+%2B+5%2F%28x%2B2%29+=+4x%5E2%2F%28%28x%2B2%29%28x-2%29%29+

Now you should be able to see that the lowest common denominator for the three rational expressions (fractions) that comprise your equation is %28x%2B2%29%28x-2%29.

So:


Now that all of the denominators are the same, you can just add the numerators together, just like any other fraction addition problem. First, distribute and remove parentheses:




And add the opposite of the right hand side of the equation to both sides:
%28-4x%5E2%2B%283x%2B6%29%2B%285x-10%29%29%2F%28%28x%2B2%29%28x-2%29%29=+0

Now collect like terms:
%28-4x%5E2%2B8x-4%29%2F%28%28x%2B2%29%28x-2%29%29=+0

Now is a good time to note that either 2 or -2 would make the denominator 0, if either of these numbers comes up as a possible solution to the problem, we have to exclude those values. The solution set of an equation cannot have an element that makes any expression that is part of the equation undefined.

Keeping that in the back of our mind, recognize that a%2Fb=0 if and only if a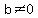=0 and b%3C%3E0. That means that the solution to our equation can be found by setting the numerator equal to zero and solving the quadratic for all possible values of x.

-4x%5E2%2B8x-4=0

Divide by -4:
x%5E2-2x%2B1=0

Since -1+%2A+-1+=+1 and -1+%2B+%28-1%29=-2, we can say that x%5E2-2x%2B1=%28x-1%29%28x-1%29=0. Therefore x-1=0 or x-1=0 so x=1 or x=1

Since neither of these results is 2 or -2, we don't have to worry about a zero denominator. Therefore the roots of the equation consist of the value 1 with a multiplicity of 2, which is the same as saying there are two real and identical roots.