SOLUTION: its me again please help me thank you for help Use long division to divide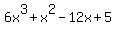{{{6x^3+x^2-12x+5}}} by {{{3x-4}}}

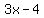
Start with this:

       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5


6x³ divided by 3x gives 2x², so write that above the
top line, above the x² term:

               2x² 
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         
Now multiply 2x² by 3x - 4 getting 6x³ - 8x²
and write this at the bottom and draw a line      


               2x² 
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
        
Now subtract.  (6x³ + x²) - (6x³ - 8x²) getting 9x²
Write this below the bottom line and bring down the
next term, which is " - 12x "

               2x² 
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x

Next, divide 9x² by 3x, getting 3x.  Write this above
the top line to the right of the 2x² and above -12x 

            
                           
               2x² +  3x
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               
Now multiply 3x by 3x - 4 getting 9x² - 12x
and write this at the bottom and draw a line

               2x² +  3x 
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               9x² - 12x
               ---------

Now subtract.  (9x² - 12x) - (9x² - 12x) getting 0.
But if it hadn't been 0 it would have been a number
times x, so write it as 0x below the bottom line and
bring down the next term, which is " + 5 "


               2x² +  3x 
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               9x² - 12x
               ---------
                      0x + 5
                   
Next, divide 0x by 3x, getting 0.  Write this above
the top line to the right of the 3x and above + 5 



               2x² +  3x + 0
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               9x² - 12x
               ---------
                      0x + 5

Now multiply 0 by 3x - 4 getting 0x - 0
and write this at the bottom and draw a line



               2x² +  3x + 0
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               9x² - 12x
               ---------
                      0x + 5
                      0x - 0
                      ------
                           
Finally subtract.  (0x + 5) - (0x - 0) getting 5
Write this below the bottom line.  

               2x² +  3x + 0
       ---------------------  
3x - 4 ) 6x³ +  x² - 12x + 5
         6x² - 8x²
         ---------
               9x² - 12x
               9x² - 12x
               ---------
                      0x + 5
                      0x - 0
                      ------
                           5

There are no more terms to bring down 
so we are done except for interpreting
the answer.

The 3x - 4 is called the divisor, the
2x² +  3x + 0 is called the quotient,
and the 5 at the bottom is called the
remainder.

We interpret the answer by the formula





Or getting rid of the 0,




Edwin