|
Question 131500: Find the vertex, the line of symmetry, the maximum or minimum value of the quadratic function, and graph the function.
f(x) = -x^2 + 4x + 6
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The x-coordinate of the vertex of a parabola in the form  is given by is given by 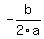 . .
The y-coordinate is then 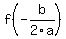 . .
The line of symmetry passes through the vertex, so the equation is  . .
The maximum or minimum is the value of the function at 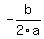 . Whether it is a maximum or minimum depends on whether the parabola opens up or down. If it is concave up (makes a valley rather than a hill), the point is a minimum, otherwise it is a maximum. You can tell which way the parabola opens by the sign on the lead coefficient. if . Whether it is a maximum or minimum depends on whether the parabola opens up or down. If it is concave up (makes a valley rather than a hill), the point is a minimum, otherwise it is a maximum. You can tell which way the parabola opens by the sign on the lead coefficient. if 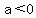 , it is concave down, if , it is concave down, if  , it is concave up, and, of course, if , it is concave up, and, of course, if  you don't have a parabola at all. you don't have a parabola at all.
Let's look at your specific problem:

First thing to note is that 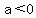 , so this is a concave down parabola and the vertex is a maximum. , so this is a concave down parabola and the vertex is a maximum.
 , so the x-coordinate of the vertex is , so the x-coordinate of the vertex is  and the equation of the line of symmetry is and the equation of the line of symmetry is  . .
The value of the function at 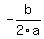 , denoted , denoted 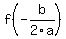 for your problem is for your problem is 
So the y-coordinate of the vertex and the maximum value of f is 

|
|
|
| |