SOLUTION: For the following systems of linear equations: a) Determine how many solutions exist b) Use either elimination or substitution to find the solutions (if any) c) Graph the two l

5x + 6y = 1 and x + 7y = 2 

Let's use elimination:

5x + 6y = 1  
 x + 7y = 2

Multiply the bottom equation by -5 to eliminate the x's

 5x +  6y =   1  
-5x - 35y = -10
---------------
     -29y =  -9
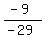        y = 
        y =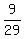 

Since the answer is complicated, start over

5x + 6y = 1  
 x + 7y = 2

This time eliminate the y's by multiplying the 
first equation through by -7 and the second one 
through by +6:

-35x - 42y = -7  
  6x + 42y = 12
---------------
-29x       =  5
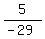   x       = 
         x =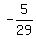 

c) Graph the two lines, labeling the x-intercepts, 
y-intercepts and points of intersection. 

Find the x-intercept by substituting 0 for y and
solving for x

  5x + 6y = 1
5x + 6(0) = 1
   5x + 0 = 1
       5x = 1
        x = 

So the x-intercept is the point (,0)

Find the y-intercept by substituting 0 for x and
solving for y

  5x + 6y = 1
5(0) + 6y = 1
   0 + 6y = 1
       6y = 1
        y = 

So the y-intercept is the point (0,)

Get some points on the first line:

(-7,6), (-1,1), (5,-4)

Plot them and draw a line through them:



The x- and y-intercepts are so close together and
so close to the origin it is impossible to label
them on this graph.  We'll zoom in on it later.

Now let's draw the second line:

Find the x-intercept by substituting 0 for y and
solving for x

  x + 7y = 2
x + 7(0) = 2
   x + 0 = 2
       x = 2
 
So the x-intercept is the point (2,0)

Find the y-intercept by substituting 0 for x and
solving for y

   x + 7y = 2
 (0) + 7y = 2
       7y = 2
        y = 
    
So the y-intercept is the point (0,)

Get some points on the second line:

(-5,1), (2,0), (9,-1)

Plot them and draw a line through them:



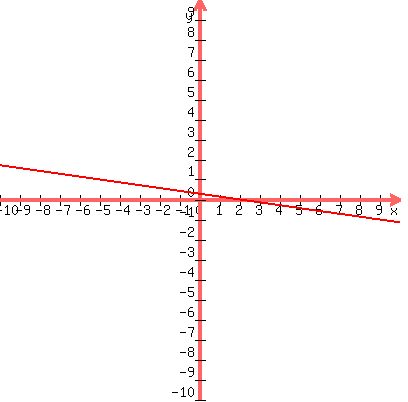Now we put them both on the same graph



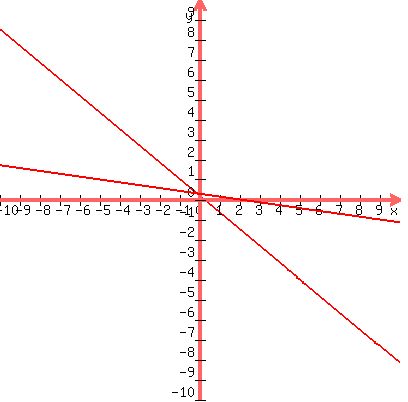It's too hard to label everything on
that graph, because all those points are
scrunched up together near the origin, 
so let's zoom in on a small section of
the graph:



point A is the x-intercept of the first line, (,0)
point B is the y-intercept of the first line, (0,)
point C is the x-intercept of the second line, (2,0)
point D is the y-intercept of the scond line, (0,)
point E is their point of intersection, (,)

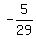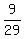Edwin