I can't seem to figure out this problem. Could I please have some help in
figuring it out. Bobby and Mike have a summer job mowing the school yard. One
riding mower takes 7 hours and the other takes 6 hours. If they are both used
to mow the yard, how long will it take.
Here's how to do it without algebra. Then we'll do it with algebra.
If both mowers were to run continually for 42 hours, the 7-hr mower would have
mowed 6 lawns and the 6-hour mower would have mowed 7 lawns, a total of 13
lawns. So it takes them both together 42 hours to mow 13 lawns, then dividing
42 by 13, it takes them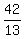 
or 
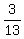hours to mow 1 lawn.
With algebra:
Make this chart:
No. of lawns Rate in lawns/hr Time
Slower mower
Faster mower
Both together
Let x be the answer, the time for both together to mow 1 lawn.
So fill in x for the time for "both together" and 1 for the No. of lawns.
No. of lawns Rate in lawns/hr Time
Slower mower
Faster mower
Both together 1 x
>>...One riding mower takes 7 hours and the other takes 6 hours...<<
So fill in the slower mower's time as 7 hrs and the faster mower's time
as 6 hours. Also since this is their time for mowing 1 lawn, fill in
1 for the No. of lawns.
No. of lawns Rate in lawns/hr Time
Slower mower 1 7
Faster mower 1 6
Both together 1 x
Next, use 
to fill in
the three rates:
No. of lawns Rate in lawns/hr Time
Slower mower 1 
7
Faster mower 1 
6
Both together 1 
x
Now we form the equation by:
[Rate of slower] + [Rate of faster] = [Rate of both together]
Can you solve that? If not post again asking how.
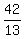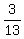Answer: or hrs.
Edwin
