SOLUTION: I am having trouble with this question it asks: The sum of a number and its reciprocal is 10. What is the number? It also says I need to cheack. - 3 Please and Thank You=)

Algebra ->  Real-numbers -> SOLUTION: I am having trouble with this question it asks: The sum of a number and its reciprocal is 10. What is the number? It also says I need to cheack. - 3 Please and Thank You=)      Log On


   

Question 130944This question is from textbook algebra
: I am having trouble with this question it asks:
The sum of a number and its reciprocal is
10. What is the number? It also says I need to cheack.
-
3
Please and Thank You=) This question is from textbook algebra

Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Let x=unknown number


So if the sum of the unknown number and it's reciprocal is 10%2F3, then we have the equation


x%2B1%2Fx=10%2F3


3x%28x%2B1%2Fx%29=3x%2810%2F3%29 Multiply both sides by 3x. Doing this will eliminate the fractions


3x%5E2%2B3=10x Distribute and multiply


3x%5E2-10x%2B3=0 Subtract 10x from both sides


%28x-3%29%283x-1%29=0 Factor the left side


x-3=0 or 3x-1=0 Set each factor equal to zero


x=3 or x=1%2F3 Solve each equation for x


So our numbers are

x=3 or x=1%2F3




Check:
Let's check x=3

3%2B1%2F3=10%2F3

9%2F3%2B1%2F3=10%2F3

10%2F3=10%2F3 Works

----------

Let's check x=1%2F3

1%2F3%2B1%2F%281%2F3%29=10%2F3

1%2F3%2B3=10%2F3

1%2F3%2B9%2F3=10%2F3

10%2F3=10%2F3 Works


Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
x is the number. The reciprocal of a number is also called the multiplicative inverse. If you multiply a number by its reciprocal, the result is 1.

So, the reciprocal of x is 1%2Fx because x%281%2Fx%29=1.


The sum of two things is what you get when you add them together.


The sum of a number, x, and its reciprocal 1%2Fx, is (=) 10.

x+%2B+1%2Fx=10

The common denominator is x, so:

%28x%5E2%2B1%29%2Fx=10

x%5E2%2B1=10x

x%5E2-10x%2B1=0

There are no rational factors, i.e. there is no p and q such that pq = 1 and p + q = -10. Therefore, either complete the square or use the quadratic formula.

Complete the square:
x%5E2-10x=-1

x%5E2-10x%2B25=24

%28x-5%29%5E2=24

x-5=sqrt%2824%29 or x-5=-sqrt%2824%29

x=5%2B2sqrt%286%29 or x=5-2sqrt%286%29

Or use the quadratic formula: x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

x+=+%28-%28-10%29+%2B-+sqrt%28+%28-10%29%5E2-4%2A1%2A1+%29%29%2F%282%2A1%29+

x+=+%2810+%2B-+sqrt%28+96+%29%29%2F2+

x=%2810%2B4sqrt%286%29%29%2F2 or x=%2810-4sqrt%286%29%29%2F2

x=5%2B2sqrt%286%29 or x=5-2sqrt%286%29 Same result.

Check the answer:
x%2B1%2Fx=10, so plug in the 1st value for x:

%285%2B2sqrt%286%29%29%2B1%2F%285%2B2sqrt%286%29%29=10

In order to add these two quantities you need to rationalize the denominator for the fraction part. Rationalizing the denominator means to get rid of the radical in the denominator expression. The technique here is to remember the factorization of the difference of two squares, %28a%2Bb%29%28a-b%29=a%5E2-b%5E2.

So we need to multiply the fractional part by 1 in the form of 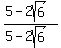%285-2sqrt%286%29%29%2F%285-2sqrt%286%29%29.



%285%2B2sqrt%286%29%29%2B%28%285-2sqrt%286%29%29%2F%285%5E2-%282sqrt%286%29%29%5E2%29%29=10

Answer checks.

Now all you have to do is check the other value for x. I'll let you handle that.