Question 130353: A closed box has square ends and a surface area of 10 square feet. The closed box's length is x, its width 6-x and its height 5-x.
a) Find the equation for the volume of this box
b) Use your polynomial to find the maximum volume of this box
c) What are the dimensions of this box?
Can you help me with this step by step? It will be much appreciated. I apologize for the three parts of the problem that is to be answered.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Right off the bat, there is something fishy with your problem description. Either your contention that the ends of the box are square is in error, or you have misstated the definition of the dimensions of the box. For the end of the box to be square, two of the dimensions must be identical, but as stated, they are all different. I'm going to proceed on the assumption that you meant that the box has rectangular ends.
a) The volume of a rectangular solid is given by  . Using the dimensions given, the volume of your box is . Using the dimensions given, the volume of your box is  . Expanding this yields: . Expanding this yields:


b)  is the volume function. The volume function has a local extrema at the point where the first derivitive equals zero. So: is the volume function. The volume function has a local extrema at the point where the first derivitive equals zero. So:
 . Set this equal to zero and solve. . Set this equal to zero and solve.
 . .



So:  or or  . However, . However,  which would make the height which would make the height 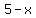 a negative value. Therefore exclude this root. That means an extreme volume is obtained when a negative value. Therefore exclude this root. That means an extreme volume is obtained when  . But is it a maximum or minimum? If the value of the second derivitive is negative at the x-coordinate of the extreme point, then the point is a maximum. . But is it a maximum or minimum? If the value of the second derivitive is negative at the x-coordinate of the extreme point, then the point is a maximum.
 . Since . Since 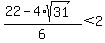 , the second derivitive at this point is clearly negative. The function is a maximum at this point. , the second derivitive at this point is clearly negative. The function is a maximum at this point.
Now that we know the value of x that produces the maximum volume, we need to find the value of the Volume function at that value of x, so:

Now if you want, you could expand all that and simplify it to a single radical expression, but I'm just going to take an approximation of the value and calculate it that way.

 cubic feet approximately. cubic feet approximately.
c) The surface area of a closed box is given by  . Substituting the given values for length, width, height, and surface area we have: . Substituting the given values for length, width, height, and surface area we have:





 (exclude the negative root because we are calculating a physical length) (exclude the negative root because we are calculating a physical length)
Oh No! Danger! Warning, Will Robinson!! We have an impossible situation. The height of the box is 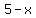 , but if , but if  , that means the height is 0. Hence, we have no box. This is another indication that you messed up on the problem statement because a box with dimensions of x, 6 - x, and 5 - x, cannot have a surface area of 10 square units and still be a box with an actual volume. , that means the height is 0. Hence, we have no box. This is another indication that you messed up on the problem statement because a box with dimensions of x, 6 - x, and 5 - x, cannot have a surface area of 10 square units and still be a box with an actual volume.
On the other hand, if the question actually asks for the dimensions of the maximum volume box, then just take the value for x we determined in part b, subtract it from 6, then subtract it from 5, and you will have your three dimensions.
|
|
|