Question 129835: Two towns are 243 miles apart. Bob and Joe each start in on of the towns at 12:00 PM and drive towards each other with uniform motion. Bob drives 45mph, joe drives 65 mph. When do they meet (at what time)? WHERE do they meet?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember  , so , so  . .
Since we are interested in when and where they meet, their drive times must be equal.
Let's say that x is the distance Bob drives at 45 mph. That means that the distance Joe drives at 65 mph is 243 - x.
Using  , Bob's drive time is , Bob's drive time is  , and Joe's drive time is , and Joe's drive time is  . But we already determined that these drive times are equal so we can say: . But we already determined that these drive times are equal so we can say:
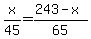
Cross multiply:



From here on out, '=' means 'approximately equal to'
 , or Bob drove , or Bob drove 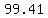 miles to the meeting point. miles to the meeting point.
Since we know that  , Bob's travel time must be , Bob's travel time must be  or or  hours. hours.  hours is hours is  minutes, and since they started at straight up noon, they must have met at 2:12.6 PM, and they met 99.41 miles from Bob's starting point. minutes, and since they started at straight up noon, they must have met at 2:12.6 PM, and they met 99.41 miles from Bob's starting point.
Check:
Since they met at 99.41 miles from Bob's starting point, they must have met 243 - 99.41 = 143.59 miles from Joe's starting point. If Joe travelled for 2.21 hours at 65 mph, he travelled  miles. Answer checks. (Actually, if you just plug in the numbers given, the calculator shows a bit of error, but if you do the arithmetic from the beginning on the calculator and never round off until the end, it all comes out correctly) miles. Answer checks. (Actually, if you just plug in the numbers given, the calculator shows a bit of error, but if you do the arithmetic from the beginning on the calculator and never round off until the end, it all comes out correctly)
|
|
|