Question 129832: This is not out of a textbook. The problem is to determine the weight of an object in various places using the following equation: w - Cr^-2, where C is a constant, and r is the distance that the object is from the center of the earth.
a. Solve the equation w = Cr^-2 for r.
b. Supposed that an object is 100 pounds when it is at sea level. Find the value of C that makes the equation true. (Sea level is 3,963 miles from the center of the earth.)
c. Use the value of C you found in the previous question to determine how much the object would weigh in:
Death Valley (282 feet below sea level)
The top of Mt. McKinley (20,430 feet above sea level)
I am totally confused and there are several other parts to the question that I won't be able to do unless I understand these parts.
I appreciate any help you can give.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Part a: "Solve for (something)" means to do whatever is legal to get that something all by itself on one side of the equal sign (typically the left because we read left to right) and everything else on the other side.

Remember that  , so the equation becomes: , so the equation becomes:

Multiply both sides by 

And divide both sides by w

And finally take the square root of both sides. We only need the positive square root because we are interested in a radius which is a distance.

And that's all there is to that.
Part b: Here you need to solve the equation for C and then plug in the values of 100 for weight and 3963 for r at sea level. We could start over from the original equation, but let's take the easy way and go back to an intermediate result that we obtained doing part a:  , which can be written: , which can be written:



Part c:
Here's where you need to be careful with your units. Death Valley is 282 FEET below sea level, but the earth's radius is given in miles. Now we could either convert 282 feet to miles, or 3963 miles to feet. The first way, the numbers are going to be a horror, but the second way, they will be sublimely ridiculous, so let's go with the lesser of two evils.
 (approximately, and plenty close enough) (approximately, and plenty close enough)
That means that the radius in Death Valley has to be 
So, using the original formula:



So if something weighs 100 lbs at sea level, it will gain three thousanths of a pound if you take it to Death Valley.
The Mt. McKinley part is done the same way, just different numbers:
 (close enough) (close enough)
So the radius becomes 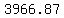 and and


I'll let you do the calculator work from here.
Super-Double-Plus Extra Credit: I'm a big boy, I weigh in at 260. So how much would I weigh in Death Valley? Hint: Since you gain .003 lbs on 100 lbs, that means the gain is .003%.
|
|
|