Question 129798: There are two boxes labeled “A” and “B.” Note on the box “A” reads: The note on the box “B” is true and gold is in the box “A.” Note on the box “B” reads: The note on the box “A” is false and gold is in the box “A.” You have only one chance to open a box to get gold. Which box would you open and why?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm going to establish some symbology for this discussion.
 is the note on A, is the note on A,  is the note on B, is the note on B,  is "the gold is in box A", is "the gold is in box A",  is "the gold is in box B" is "the gold is in box B"
Also, since I can't figure out how to render a vinculum on this system, I'm going to denote the idea of 'Not' by prefacing the above symbols with an  . .  = 'not the note on A' which is equivalent to 'the note on A is false' Also & means 'and', v means 'or', T means True, and F means False. And lastly, a => b, means 'if a then b' = 'not the note on A' which is equivalent to 'the note on A is false' Also & means 'and', v means 'or', T means True, and F means False. And lastly, a => b, means 'if a then b'
 & &
 & &
Let's begin by assuming  . .
If  then then  , but if , but if  then then  . This is a contradiction. Therefore . This is a contradiction. Therefore 
 => =>  v v 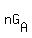
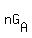 => =>  . Let's save this result for later. . Let's save this result for later.
 => =>  (not not (not not  ) v ) v 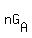
We have already proven  , so for , so for  to be true, to be true, 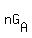 must be true, and, again, must be true, and, again, 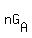 => =>  . .
Therefore, the gold is in Box B.
|
|
|