Question 129457: Suppose that you take all of the black cards out of a standard deck of 52 cards and thoroughly shuffle the remaining 26 red cards. From this deck of 26 red cards you will select 3 cards, one at a time, WITHOUT replacement, and record weather each card is picked is a face card (a jack, queen, or king), or not a face card.
a.) What is the probability that none of the 3 cards picked in this way is a face card?
b.) what is the probability that exactly one of the three cards picked is a face card?
Answer by Edwin McCravy(20059)   (Show Source):
You can put this solution on YOUR website! Suppose that you take all of the black cards out of a standard deck of 52 cards
and thoroughly shuffle the remaining 26 red cards. From this deck of 26 red
cards you will select 3 cards, one at a time, WITHOUT replacement, and record
weather each card is picked is a face card (a jack, queen, or king), or not a
face card.
The sample space is
AH,2H,3H,4H,5H,6H,7H,8H,9H,10H,JH,QH,KH
AD,2D,3D,4D,5D,6D,7D,8D,9D,10D,JD,QD,KD
It contains 6 face cards and 20 non-face cards.
"AND" means "multiply"
"OR" means "add".
a.) What is the probability that none of the 3 cards picked in this way is a
face card?
P(picking a non-face card first AND a non-face card second AND a non-face card
third) =
P(picking a non-face card first) x P(picking a non-face card second) x
P(picking a non-face card third) =
 = 
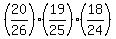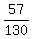
b.) what is the probability that exactly one of the three cards picked is a
face card?
P[(face card 1st AND non-face card 2nd AND non-face card 3rd) OR
(non-face card 1st AND face card 2nd AND non-face card 3rd) OR
(non-face card 1st AND non-face card 2nd AND face card 3rd)] =
P(face card 1st) x P(non-face card 2nd) x P(non-face card 3rd) +
P(non-face card 1st) x P(face card 2nd) x P(non-face card 3rd) +
P(non-face card 1st) x P(non-face card 2nd) x P(face card 3rd) =
 =
=
------------------------
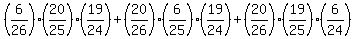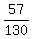Notice that the two answers happened to come out the same.
Edwin
|
|
|
