Question 129145: I have to solve this problem by the addition method. I do have a book but this problem is not out of a book,it's from a handout. I tried to follow the steps in the book to do this but its not clear enough for me.I'm not sure how to go about doing this.Do I just add them together and then plug in numbers that are given? The problem is:


The choice for answers are: A) (3,2) B)(-2,3) C)(3,-2)D)(-3, 5/2) E)(none of them)
I chose NONE OF THE ABOVE.
Thankyou so much!
Answer by Construe(3)   (Show Source): (Show Source):
You can put this solution on YOUR website! Edit: 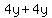 does not always equal does not always equal  , but , but  always. That is what we are doing when we take Equation 1 minus Equation 2. To illustrate my point, I will show it step-by-step: always. That is what we are doing when we take Equation 1 minus Equation 2. To illustrate my point, I will show it step-by-step:

Simplify the 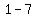 on the right side of the =. on the right side of the =.

Remove unnecessary brackets (or parentheses, depending on what you want to call them).

Now we remove the other pair of brackets. However, the sign before the open bracket is a minus sign, so we change the + sign inside the bracket to a -.

To understand why we must change the sign, consider this example. Let x be apples and y be oranges. When I perform 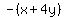 , I am taking away 1 apple and 4 oranges. That would have the same effect as taking away 1 apple, , I am taking away 1 apple and 4 oranges. That would have the same effect as taking away 1 apple,  , and then taking away 4 oranges, , and then taking away 4 oranges,  , so: , so:

We have  . .
Rearranging the terms,

Simplifying x,

Obviously +4y and -4y cancel each other out, so our final equation is


---
We are given two equations:
Equation 1:
Equation 2:
Subtracting Equation 2 from Equation 1, we obtain:



Then, substitute  into Equation 2: into Equation 2:



Since  and and  , the solutions of ( , the solutions of ( , , ) are ( ) are ( , , ), and the answer is ), and the answer is  . .
|
|
|