Question 12890: The equation |x-1|+|x-2|+|x-3|=4 has two solutions what are they?
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! |x-1|+|x-2|+|x-3|=4
Note 1,2 and 3 divide the real line into four parts (intervals )
nameley, (-oo,1),[1,2),[2,3) & [3,+oo)
case (i) when  , we get x-1+ x-2+ x-3=4 , we get x-1+ x-2+ x-3=4
or 3x = 10, so x = 10/3 ({{>= 3}}} OK.
case (ii) when  , we get x-1+ x-2 -(x-3)=4 , we get x-1+ x-2 -(x-3)=4
or x = 4. Since 4 is not in [2,3), invalid answer.
case (iii) when  , we get x-1 -(x-2) -(x-3)=4 , we get x-1 -(x-2) -(x-3)=4
or -x + 4 = 4 so x = 0. Since 0 is not in [1,2), invalid answer.
case (iv) when 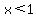 , we get -(x-1)-(x-2) -(x-3) =4 , we get -(x-1)-(x-2) -(x-3) =4
or -3x = -2, so x = 2/3. Since 2/3 is not in (-oo,1), invalid answer.
Hence, there is only one solution x = 10/3.
Try to read carefully about the details.
Sorry, I will not give further explanations for this simple questions.
The reason I solved it for you is to aviod that you may get long solutions.
Kenny
|
|
|