Question 128896: g(x)=(2x^2-2)/(x^2+3x)
How do I find... Domain for g? Vertical asymptote of g, horizontal asymptote, x and y intercept. THanks for help in advance!
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The domain of a function is all values for which the function is defined. Since this is a rational function, we need to examine the denominator and exclude any values from the domain that would make the denominator be zero.
The denominator of this function, 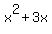 factors to factors to 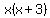 , so we know that we must exclude , so we know that we must exclude  and and  because either of these values would make the denominator zero. because either of these values would make the denominator zero.
Therefore the domain of g is the set of all x such that x is a real number,  , and , and 
Vertical asymptotes for a rational function exist wherever you have a value that is excluded from the domain. The equation of a general vertical line is  where a is the x-coordinate of any point on the line. So for this function, there are vertical asymptotes at where a is the x-coordinate of any point on the line. So for this function, there are vertical asymptotes at  and and  . .
Horizontal asymptotes are horizontal lines that are approached but not reached as the absolute value of x becomes very large. There is at most one horizontal asymptote for any given rational function.
If the degree of the denominator polynomial is larger than the degree of the numerator polynomial, then there is a horizontal asymptote at  . .
If the degree of the denominator polynomial is less than the degree of the numerator polynomial, then there is no horizontal asymptote. If the difference in degree does not exceed 1, then there is a slant asymptote. The equation of the slant asymptote can be found by using polynomial long division to divide the numerator by the denominator. The slant asymptote will then be the quotient excluding any possible remainder.
If the degrees of the denominator and numerator polynomials are equal, then there is a horizontal asymptote at  where a is the lead coefficient on the numerator polynomial and b is the lead coefficient on the denominator polynomial. The lead coefficient on a polynomial is the coefficient on the highest order term. where a is the lead coefficient on the numerator polynomial and b is the lead coefficient on the denominator polynomial. The lead coefficient on a polynomial is the coefficient on the highest order term.
For your problem, both the denominator and numerator are degree 2. The lead coefficient on the numerator is 2 and the lead coefficient on the denominator is 1, so the equation of the horizontal asymptote is 
The y-intercept of a function can be found by letting x = 0. However, for this function, 0 is excluded from the domain of the function. Therefore, there is no y-intercept for this function.
The x-intercept(s) is/are the value(s) of x that make g(x) = 0. Since  if and only if if and only if  and and 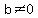 , then we only need to set the numerator equal to zero, solve, and then exclude roots that are not in the domain of the function, if any. , then we only need to set the numerator equal to zero, solve, and then exclude roots that are not in the domain of the function, if any.



 or or  . Neither of these potential roots of the function are excluded from the domain, so both of them are roots and therefore x-intercepts. . Neither of these potential roots of the function are excluded from the domain, so both of them are roots and therefore x-intercepts.
Let's look at a picture and see if our analysis looks right or not:

Yep, it is very large or very small when near x = -3 and x = 0. It looks like it will flatten out and approach y = 2 as x gets very large or very small, and it corsses the x-axis at 1 and -1.
|
|
|