SOLUTION: I'm doing solving and graphing inequalities y>2x+3 I have solved a different problem y+4 is greater than or equal to 6 by subtracting 4 from both sides and got the answer y is gr

Algebra ->  Graphs -> SOLUTION: I'm doing solving and graphing inequalities y>2x+3 I have solved a different problem y+4 is greater than or equal to 6 by subtracting 4 from both sides and got the answer y is gr      Log On


   

Question 12876: I'm doing solving and graphing inequalities y>2x+3
I have solved a different problem y+4 is greater than or equal to 6 by subtracting 4 from both sides and got the answer y is greater then or equal to 2. But I do not know where to begin with y>2x+3. Please help me explain it to my 13 year old. Thanks in advance. Karen.
Answer by AdolphousC(70) About Me  (Show Source):
You can put this solution on YOUR website!
This is similar to graphing Linear Equations of the form y = mx + b. There are only two differences, first, after you plot 2 points, you need to determine weather the line is dashed or solid, then where to shade. But graphing is the same.


The first thing you need to do is plot your y-intercept ( where the line crosses the y-axis ) this would be at +3 since the equation is y > 2x + 3.


Now we know the slope is 2 or 2/1, so using Rise/Run, you are going to start at your y-intercept, move up two spaces and right 1, so you should now be at the point (1,5)


Determining if the line is shaded or not just takes a quick glance at the sign of the equation. If the sign is just Greater Than or Less Than the line will be dashed, however, if it is a Greater Than or Equal To, or Less Than or Equal To it will have to be solid.


Now as for the shading part, what you want to do is choose a point that is NOT on your line, in most cases ( 0,0 ) is the best choice because its easy, but this will ONLY work if the line does not pass through this point, for this problem our line does NOT pass through ( 0,0 ) so we are going to choose that point.


Now, Substitute the x value for x and the y value for y, and simplify ( see below)
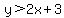+y+%3E+2x+%2B+3+ Substitute
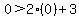+0+%3E+2%280%29+%2B+3+ Simplfy each side of the equation
+0+%3E+3+
Now you need to ask your self a question, does this make sense? Is 0 > 3, of course not, so you need to shade on the side of the line that does NOT include (0,0) in this case you would shade ABOVE the line...


If the statement made sense, say 0 < 3, then you would want to shade BELOW the line, or shade towards the point that gave you the true solution.
Hope this helps. Mr. C