|
Question 128663This question is from textbook beginning algebra
: Thank you for taking the time to help me on my lovely algebra headache homework. Your time is very much appreciated! Now on to the equation issue.
(((2x+1/5y=6))) a.(?,20) b.(9/5,?) I need help in finding the missing coordinates please walk me through this problem in hope I can grasp this linear equation stuff before it spirals out of control. Thank you once again for your time and efforts.
This question is from textbook beginning algebra
Found 2 solutions by solver91311, bucky:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! 
Look at your equation as a rule for describing a set of points that lie in a straight line -- hence the term, 'linear' equation. By writing the equation, you have created a relationship between the equation and that set of points such that if you substitute the x- and y-coordinate values from any point that IS on the line back into the equation, you will get a true statement. On the other hand, if you substitute the x- and y-coordinates from a point that IS NOT on the line, you will get a false statement.
Let's use a simple example to illustrate the concept. We'll use  . The point (1,2) lies on the line, and we know this for sure because if we substitute the number 1 for x and the number 2 for y in the equation, we get  or just  which we know to be a true statement. But let's look at the point (5,1). If we substitute the x-coordinate, 5, and the y-coordinate, 1 into the equation we get  or  , clearly a false statement. So we can say with certainty that the point (5,1) does not lie on the line.
For your problem, you are faced with having to determine, for part a, what value of x will make the equation  true whenever y has the value 20. So let's put 20 into the equation and see what happens:
You should be able to tackle part b by yourself now. Write back if you are still stuck.
Answer by bucky(2189)  (Show Source):
You can put this solution on YOUR website! Sure you can grasp this.
.
The fundamental thing you need to understand is that coordinate points are always of the
form (x, y). So the first value inside the parentheses is the value of x and the second value
(after the comma) is the value of y. So the point (?, 20) tells you that you don't know the
value of x, but the value of y is 20. So, you go to the equation:
.
.
and you substitute 20 for y and then you solve for x. Substituting 20 for y in the equation
results in:
.
.
And one-fifth of 20 is 4 which further reduces the equation to:
.
.
Get rid of the 4 on the left side by subtracting 4 from both sides and you have:
.
.
Finally solve for x by dividing both sides of this equation by 2, the multiplier of x, and
you get:
.
.
So you now know that when y equals 20, x equals -1. So the coordinate point you are looking
for is (1, 20)
.
In the second part of this problem you are given the point (9/5, ?}. This tells you
that  and you are to solve for y. Go to the equation again and this time substitute
 for x and solve for y. The original equation was:
.
.
Substitute for x and you have:
.
.
Multiply the 2 times and you get 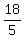 making the problem become:
.
.
Get rid of the  on the left side by subtracting from both sides, making
the equation become:
.
.
You can now get rid of the  on the left side by multiplying both sides of this equation
(all terms in the equation) by 5 to make the equation become:
.
.
Now just solve for y by algebraically combining the two terms on the right side to get:
.
y = 12
.
So the answer to the second problem is that the coordinate point is (9/5, 12)
.
Hope this helps to cure your headache.
.
|
|
|
| |
