Question 128256: My teacher want us to expand the following binomials. I did not understand the "easy" way and we do not have enough textbooks at my school to take one home. Please give me as much detail as you can on how to solve this type of problem 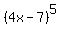
Thank you,
Found 2 solutions by solver91311, checkley71:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The easy way if your exponent is less than 10 or so, is to use Pascal's
Triangle to develop your coefficients, and then just fill in the pattern.
You need the first 6 rows of Pascal's Triangle to do a 5th degree expansion:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
So if you had 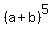 , the expansion would be: , the expansion would be:
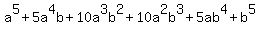
Notice that the coefficients are just the last row of Pascal's Triangle, the
exponent on a starts at 5 and goes down by one per term until you get to the
last term where a disappears because the exponent is 0 (remember,  ) )
and the exponent on b starts at 0 and increases by 1.
Now all you have to do is take the expansion above and replace a with 4x and b with -7

Notice that the 4 in 4x is inside the parentheses and must also be raised to the indicated power, so:
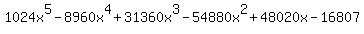
By the way, if you need to get the next or subsequent rows of Pascal's
Triangle, you start with 1 and then each number across the row is the sum of
the numbers immediately above to the right and left. The sixth row starts 1,
6, 15...
In general, the r-th coefficient of the n-th degree binomial expansion is 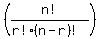
Answer by checkley71(8403)   (Show Source): (Show Source):
You can put this solution on YOUR website! (4x-7)^5 requires you to multiply (4x-7)by(4x-7) five times:
4x-7
4x-7
----------------------
16x^2-28x-28x+49 or
16x^2-56x+49
4x-7
-------------------------
64x^3-224x^2+196x-112x^2+392x-343 or
64x^3-336x^2+588x-343
4x-7
-------------------------
256x^4-1344x^3+2352x^2-1372x-448x^3+2352x^2-4116x+2401 or
256x^4-1792x^3+4704x^2-5488X+2401
4X-7
-----------------------------------------
1024X^5-7168X^4+18816X^3-21952X^2+9604X-1792X^4+32928X^3-32928X^2+39416X-16807
OR
1024X^5-8960X^4+51744X^3-54880X^2+49020X-16807 ANSWER.
|
|
|