Question 127985: This question is one question with four parts!
I asked the first part already bur I'm going to stick all four parts together on this question so that it makes sense.
1.Suppose you are in the market for a new home and are interested in a new housing community under construction in a different city.
1a.The sales representative informs you that there are two floor plans still available, and that there are a total of 56 houses available. Use x to represent floor plan #1 and y to represent floor plan #2. Write an equation that illustrates the situation.
MY ANSWER but I don't think it is right-----
x+y=56
1b. The sales representative later indicates that there are 3 times as many homes available with the second floor plan than the first. Write an equation that illustrates this situation. Use the same variables you used in part a.
MY ANSWER: 3y+x=56
1c. Use the equations from part a and b of this exercise as a system of equations. Use substitution to determine how many of each type of floor plan is available. Describe the steps used to solve the problem.
NOW for this problem I am completely lost but I'm going to give it a try-------
MY ANSWER: 3y^2+x^2=56*3 OR IS IT THIS: 3y^2+x^2=168?
1d. What are the intercepts of the equation from part a of this problem? What are the intercepts from part b of this problem? Where would the lines intersect if you solved the systems by graphing?
THIS QUESTION i'M TOTALLY STUMPED ON!.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1a.The sales representative informs you that there are two floor plans still available, and that there are a total of 56 houses available. Use x to represent floor plan #1 and y to represent floor plan #2. Write an equation that illustrates the situation.
 (a)
(a)
1b. The sales representative later indicates that there are 3 times as many homes available with the second floor plan than the first. Write an equation that illustrates this situation. Use the same variables you used in part a.
 (b)
(b)
1c. Use the equations from part a and b of this exercise as a system of equations. Use substitution to determine how many of each type of floor plan is available. Describe the steps used to solve the problem.
 (a)
(a)
 (b)
.substitute
(b)
.substitute  from this equation from (a) from this equation from (a)
---------------------------------------
 (a)
(a)




 (b)
.
(b)
.


1d. What are the intercepts of the equation from part a of this problem? What are the intercepts from part b of this problem? Where would the lines intersect if you solved the systems by graphing?
the intercepts are:
 (a)
if
(a)
if  , , 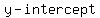 will be: will be:

 so,
so, 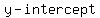 is ( is ( , , ) )
if  , ,  will be: will be:

 .so,
.so,  is ( is ( , , ) )
| Solved by pluggable solver: Graphing Linear Equations |
 Start with the given equation Start with the given equation
 Subtract Subtract 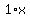 from both sides from both sides
 Multiply both sides by Multiply both sides by 
 Distribute Distribute 
 Multiply Multiply
 Rearrange the terms Rearrange the terms
 Reduce any fractions Reduce any fractions
So the equation is now in slope-intercept form ( ) where ) where  (the slope) and (the slope) and  (the y-intercept) (the y-intercept)
So to graph this equation lets plug in some points
Plug in x=0

 Multiply Multiply
 Add Add
So here's one point (0,56)

Now lets find another point
Plug in x=1

 Multiply Multiply
 Add Add
So here's another point (1,55). Add this to our graph

Now draw a line through these points
 So this is the graph of So this is the graph of  through the points (0,56) and (1,55) through the points (0,56) and (1,55)
So from the graph we can see that the slope is  (which tells us that in order to go from point to point we have to start at one point and go down -1 units and to the right 1 units to get to the next point), the y-intercept is (0, (which tells us that in order to go from point to point we have to start at one point and go down -1 units and to the right 1 units to get to the next point), the y-intercept is (0, )and the x-intercept is ( )and the x-intercept is ( ,0) . So all of this information verifies our graph. ,0) . So all of this information verifies our graph.
We could graph this equation another way. Since  this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, ). ).
So we have one point (0, ) )

Now since the slope is  , this means that in order to go from point to point we can use the slope to do so. So starting at (0, , this means that in order to go from point to point we can use the slope to do so. So starting at (0, ), we can go down 1 units ), we can go down 1 units

and to the right 1 units to get to our next point

Now draw a line through those points to graph 
 So this is the graph of So this is the graph of  through the points (0,56) and (1,55) through the points (0,56) and (1,55)
|
|
|
|