Question 127819: Daddy Warbucks always carries a specific number of $100 and $500 bills for impulse purchases and $1 bills for tips. If he has 500 bills in his briefcase and they total $50000, how many of each denomination does he carry?
Please help me, I do not know how to set this up to solve. Thankyou
My question is not from a textbook, but it is from my teacher in my Math 102, Intermediate Algebra class.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I used h for hundreds, f for five hundreds, and s for singles.
So  . .
Hundreds are worth $100, so the value of the h hundreds is 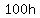 , likewise the value of the f five hundreds is , likewise the value of the f five hundreds is 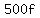 , and the value of the s singles is just , and the value of the s singles is just  , and we know that: , and we know that:

But now what? We have three unknowns but only two equations.
The secret lies in realizing that the answers must be positive integers.
Let's rearrange the equations a little:


Now multiply the first equation by -1:

And add it term-by-term to the second equation:

Then divide by 99:

Now we know that the smallest f can be is 0 and the largest it could be is 100, because  . We can actually exclude 100 because that gets us to 50,000 with only 100 bills. . We can actually exclude 100 because that gets us to 50,000 with only 100 bills.
The problem now becomes finding a whole number value for f so that the expression for h above comes out to be another whole number. You could make a list of all the results of 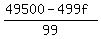 for each of the 100 possibilities for f, but that is a lot of calculator work. If you have access to MS Excel, you can solve it the way I did. I made a list of the numbers from 1 to 100, made a formula that calculated for each of the 100 possibilities for f, but that is a lot of calculator work. If you have access to MS Excel, you can solve it the way I did. I made a list of the numbers from 1 to 100, made a formula that calculated 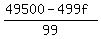 for each of those numbers, and examined the list for an integer result. for each of those numbers, and examined the list for an integer result.
There is an analysis method, but it is a bit convoluted. First thing to notice is that  , an integer, therefore we only need to find f so that , an integer, therefore we only need to find f so that 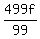 is an integer. Well, right from the start we can see that is an integer. Well, right from the start we can see that  is a possibility, but I think we can exclude that result because the wording of the problem at least implies that he has at least one of each kind of bill. is a possibility, but I think we can exclude that result because the wording of the problem at least implies that he has at least one of each kind of bill.
Now notice that, in the case of  , the remainder using integer division of , the remainder using integer division of 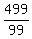 is 4. That means the remainder when is 4. That means the remainder when  will be 8, and so on until you get to will be 8, and so on until you get to  where the remainder is 96. The next one, where the remainder is 96. The next one,  , the remainder reverts to 1 , the remainder reverts to 1  , and the 'by 4' count starts over. , and the 'by 4' count starts over.  has a remainder of 97, has a remainder of 97,  => =>  , ,  => =>  , ,  => =>  , ,  => =>  , ,  => =>  !!!! And we have found the answer. !!!! And we have found the answer.
Turns out there is only one integer result, excluding the trivial result of h = 500, f = 0, and s = 0, and that is: h = 1, f = 99, and s = 400.
|
|
|