Question 127642: 2. Prove that the points (-2, 9), (-4, -2), (1, -12) and (3, -1) are vertices of a rhombus (a parallelogram with all sides equal length). Show that the diagonals are perpendicular.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
First let's find the slope of the line through the points (-2,9) and (1,-12) (these vertices are opposite from one other)
Let's denote the first point (-2,9) as ) . In other words, . In other words,  and and 
Now let's denote the second point (1,-12) as ) . In other words, . In other words,  and and 
-------------------------
 Start with the slope formula Start with the slope formula
 Plug in Plug in  , , , , , ,
 Subtract the terms in the numerator Subtract the terms in the numerator 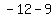 to get to get 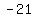 . Subtract the terms in the denominator . Subtract the terms in the denominator 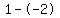 to get to get 
 Reduce Reduce
So the slope of the line through the points (-2,9) and (1,-12) is 
Now let's find the slope of the line through the points (-4,-2) and (3,-1) (these vertices are opposite from one other)
Let's denote the first point (-4,-2) as ) . In other words, . In other words,  and and 
Now let's denote the second point (3,-1) as ) . In other words, . In other words,  and and 
-------------------------
 Start with the slope formula Start with the slope formula
 Plug in Plug in  , , , , , ,
 Subtract the terms in the numerator Subtract the terms in the numerator 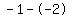 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 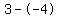 to get to get 
So the slope of the line through the points (-4,-2) and (3,-1) is 
Since the product of the two slopes is -1 (ie  ), this shows us that the two slopes are perpendicular. So the two diagonals are also perpendicular. This shows us that the figure is a rhombus. ), this shows us that the two slopes are perpendicular. So the two diagonals are also perpendicular. This shows us that the figure is a rhombus.
|
|
|