Question 127600: c. Use the value of C you found in the previous question to determine how much the object would weigh in
i. Death Valley (282 feet below sea level)
ii. The top of Mt McKinley (20,430 feet above sea level)
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given equation Start with the given equation
 Rewrite Rewrite 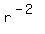 as as 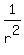
 Multiply Multiply
So we're going to use the equation  for parts i) and ii) for parts i) and ii)
i)
In order to do this problem, we need to convert 282 feet into miles. To do this, simply multiply 282 feet by 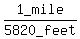 like this: like this:

So 282 feet is equivalently 0.05341 miles.
Now simply subtract 0.05341 miles from 3963 miles. We're subtracting because the distance should shrink (ie we're getting closer to the center, so the distance should be smaller)

So the distance from the center of the earth to death valley is about 3,962.94659 miles
 Start with the given equation Start with the given equation
 Plug in Plug in  and and 
 Square 3962.94659 to get 15,704,945.6751927 Square 3962.94659 to get 15,704,945.6751927
 Divide Divide
So the object now weighs 100.002695 pounds
ii)
First convert 20,430 feet to miles

So 20,430 feet is 3.86932 miles
Now add 3.86932 miles to 3963 miles. We're add because the distance should get larger (ie now we're moving away from the center, so the distance should increase)

So the distance from the center to the peak is about 3,966.86932 miles
 Start with the given equation Start with the given equation
 Plug in Plug in  and and 
 Square 3,966.86932 to get 15,736,052.2019572 Square 3,966.86932 to get 15,736,052.2019572
 Divide Divide
So the object now weighs 99.805013 pounds
|
|
|