Question 12742: The directions say to factor as completely as possible
(x-5)^3 -1
The answer is (x-6) (x^2 -9x +21)
I cannot figure out how to get this answer. Can you please show the steps?
Answer by glabow(165)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, expand the expression 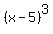 and subtract 1. and subtract 1.
This is 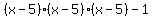
This gives 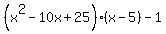
Then 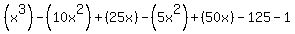
And finally 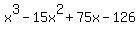
Now you factor this expression. This is done most easily by using the fact that IF IT FACTORS, the factors must be factors of 126/1 [where the numerator is the coefficient of the last term and the denominator is the coefficient of the highest term]. This only applies when the coefficients of the terms are integers. So the possible factors of this expression are 126, 63, 31, 6, 2, and 1.
You check them by putting them into the expression as the value of x and see if the expression evaluates to 0. If a number n results in the expression evaluating to 0, then (x-a) is a factor. (Do you see why? x-a will equal 0, and 0 times the other factors will always be 0.)
The simple way to check these values in the expression is by synthetic substitution, which you should either look up or review if it was taught.
Anyway, checking with 6 results in "remainder" coefficients of 1, -9, 21, and 0. This means 6 is a factor, and that (x-6) evenly divides the expression. The remainder after dividing the expression by (x-6) will be 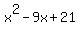 and that leaves the factors as and that leaves the factors as 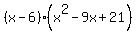
You then tackle finding factors for 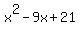
The only possible factors are 21, 7, 3, and 1. And none of them divide the expression evenly. So, there are no integer factors of the expression.
The simplest factoring of the original expression is 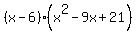
[A side note: this is a fairly complex problem unless you know the basic factor theorem and synthetic substitution. If those have not been taught to you it becomes a very difficult problem to solve.]
|
|
|