|
Question 126702: Hey again..
I'm working on the section inverse relations and functions and have a question. Heres the problem.
Find the inverse of the function y=4x-7. Is the inverse a function?
I found the inverse... its y=x+7/4 I just dont know if its a function or not?
Thank you for helping
Found 2 solutions by stanbon, bucky:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the inverse of the function y=4x-7. Is the inverse a function?
I found the inverse... its y=(x+7)/4 I just dont know if its a function or not?
------------
Your inverse equation can be written in the form y = (1/4)x +(7/4),
which is the form of a line. It is a function because for any value
you would give "x", there would be only one "y" value.
====================
Cheers,
Stan H.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Check your answer again.
.
You are given the function:
.
y = 4x - 7
.
To find the inverse of this, replace y with x and x with y to get:
.
x = 4y - 7
.
Solve this for y. Begin by transposing the equation (just swapping sides to get the term
containing y on the left side). After transposing, the equation is:
.
4y - 7 = x
.
Get rid of the -7 on the left side by adding 7 to both sides to get:
.
4y = x + 7
.
Then solve for y by dividing both sides of this equation by 4 to get:
.
y = (1/4)x + 7/4
.
This is the inverse of the function y = 4x - 7.
.
That may have been the answer you got. If so you should have written it as:
.
y = (x + 7)/4
.
so that it was clear that both terms, the x and the 7, were to be divided by 4. According to
the rules of algebra, the way you wrote the answer, only the 7 was divided by 4 and x was then
added to the result of that division so that the answer was x + (7/4).
.
Now, how do you tell whether or not that the inverse is a function? Look at the answer:
.
y = (1/4)x + (7/4)
.
This is in the form of a slope intercept equation ... the slope is (1/4) and the y-intercept
is at +7/4 on the y-axis. The graph is a straight line. ... And the graph looks like this:
.
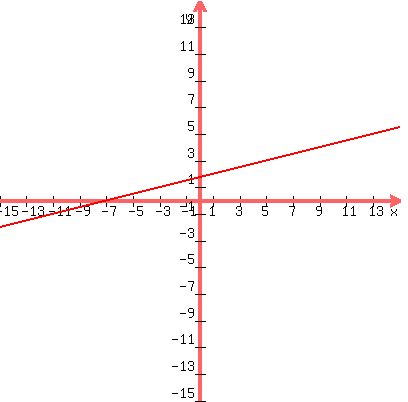
.
One way to tell if this is a function is if you can draw a vertical line anywhere on
the graph and it only intersects the graphed line at a maximum of one point, the graphed line
represents a function. On the graph shown above, anywhere you draw a vertical line it will cross the
graphed line only at one point, so you have a function. If somewhere on the graph a
vertical line could cross the graphed line at more than one point, then the graph would
not represent a function.
.
So the answer to your problem is yes ... the inverse is a function.
.
Hope this helps you to understand one way of determining whether an expression represents
a function.
.
|
|
|
| |