Question 126252: I'm stumped and need help with this Algebra problem...
Find 2 numbers that are 13 times the sum of their digits
I tried this but it does not seem to work out... can you help?
xy = 13(x+y)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let  be the two integer that are respectively 13 times be the two integer that are respectively 13 times
the sum of its digits.
Note that   be be  number (the digits are from 0-9, and 9*13=117). number (the digits are from 0-9, and 9*13=117).
Let 
Then 
We can show that M cannot be a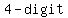 number. number.
If M is the number 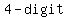 number number 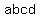 and all digits are and all digits are 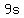 , then , then
 ….=>… not possible ….=>… not possible
Similarly, larger numbers are not possible.
We can also show that 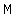 cannot be a cannot be a  number and both digits are number and both digits are 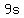 . .
If  is the number is the number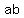 , then , then
 …. ….
=>…  … …
.=>…  … …
.=>…  ….=>… ….=>…

.=>… possible since possible since 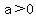 and and 
So the answers can only be  numbers. Let numbers. Let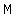 be be 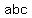 , then , then


 ……………..divide by ……………..divide by 


If  , the equation becomes , the equation becomes  . We have the following sets of solutions: . We have the following sets of solutions:
 | |  | | 
 | | | | 
 | |  | | 
 | |  | | 
If  , the equation becomes , the equation becomes  . This has no solution as the largest value of . This has no solution as the largest value of 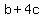 is is  (when (when  and and
 ). ).
Similarly, there is no solution for 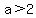
Therefore, the possible values of 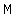 are are  , , 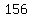 and and  . .
|
|
|