SOLUTION: Solve the system by addition or substitution. 16x – 4y = –12 y = 3 + 4x

Algebra ->  Graphs -> SOLUTION: Solve the system by addition or substitution. 16x – 4y = –12 y = 3 + 4x       Log On


   

Question 126020: Solve the system by addition or substitution.
16x – 4y = –12
y = 3 + 4x

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Solving a linear system of equations by subsitution


Lets start with the given system of linear equations

16%2Ax-4%2Ay=-12
-4%2Ax%2B1%2Ay=3

Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to choose y.

Solve for y for the first equation

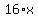-4%2Ay=-12-16%2AxSubtract 16%2Ax from both sides

y=%28-12-16%2Ax%29%2F-4 Divide both sides by -4.


Which breaks down and reduces to



y=3%2B4%2Ax Now we've fully isolated y

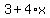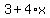Since y equals 3%2B4%2Ax we can substitute the expression 3%2B4%2Ax into y of the 2nd equation. This will eliminate y so we can solve for x.


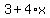-4%2Ax%2B1%2Ahighlight%28%283%2B4%2Ax%29%29=3 Replace y with 3%2B4%2Ax. Since this eliminates y, we can now solve for x.

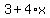
-4%2Ax%2B1%2A%283%29%2B1%284%29x=3 Distribute 1 to 3%2B4%2Ax

-4%2Ax%2B3%2B4%2Ax=3 Multiply



-4%2Ax%2B3%2B4%2Ax=3 Reduce any fractions

-4%2Ax%2B4%2Ax=3-3 Subtract 3 from both sides


-4%2Ax%2B4%2Ax=0 Combine the terms on the right side



0%2Ax=0 Now combine the terms on the left side.
0=0 Since this expression is true for any x, we have an identity.


So there are an infinite number solutions. The simple reason is the 2 equations represent 2 lines that overlap each other. So they intersect each other at an infinite number of points.

If we graph 16%2Ax-4%2Ay=-12 and -4%2Ax%2B1%2Ay=3 we get

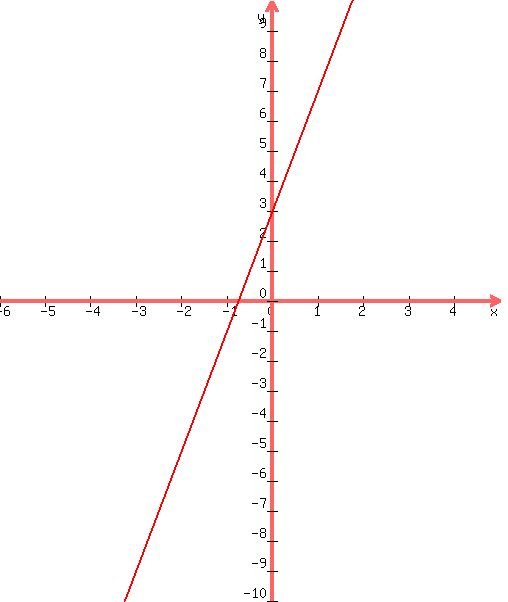+graph%28+500%2C+600%2C+-6%2C+5%2C+-10%2C+10%2C+%28-12-16%2Ax%29%2F-4%29+ graph of 16%2Ax-4%2Ay=-12


+graph%28+500%2C+600%2C+-6%2C+5%2C+-10%2C+10%2C+%283--4%2Ax%29%2F1+%29+ graph of -4%2Ax%2B1%2Ay=3 (hint: you may have to solve for y to graph these)

we can see that these two lines are the same. So this system is dependent