SOLUTION: The probability is 1 in 4,000,000 that a single auto trip in the United States will result in a fatality. Over a lifetime , an average U.S. driver takes 50,000 trips. (a) What is

We use the complement event:

P(a fatal accident over a lifetime) = 1 - P(NO fatal accident over a lifetime) 

So we consider first:

P(NO fatal accident over a lifetime) 

We are given:

P(ONE single auto trip in the United States resulting in a fatality) =
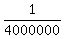 = 0.00000025

Therefore 

P(ONE single auto trip in the United States NOT resulting in a fatality) =
1-0.00000025 or 0.99999975

So

P(NO fatal accident over a lifetime) = P(NO fatal accident in the 50000 trips) = 
P(No fatality on 1st trip AND 
  No fatality on 2nd trip AND 
  No fatality of 3rd trip AND
                           ...AND
  No fatality of 49999th trip AND 
  No fatality on 50000th trip)


Since all those events are independent we can simply multiply all
their probabilities together, which amounts to raising  0.99999975 to 
the 50000th power:

and 0.9999997550000 = 0.987577799
   
But that is the probability of the complement event.

P(a fatal accident over a lifetime) = 1 - P(NO fatal accident over a lifetime)

so

P(a fatal accident over a lifetime) = 1 - 0.987577799 =

0.012422201 or rounding, about 0.0124

That's scary, isn't it?  However there is relief in
the next question:

---------------------------------

When we assume independence, we are assuming that none of 
our previous driving experiences when there were no fatal 
accidents do not make it any less likely that we will have
an accident.  We (and the insurance companies) know this 
is NOT TRUE because as a rule, we become better drivers 
when we have had more experience.  This is why the 
insurance premiums are much lower for adult drivers than
for teenage drivers.  They know that the probability of
a fatal accident decreases as we get more experience
driveing -- and become more mature.
 ----------------------------------

Well, he should not be so tempted, lest it become a habit. But if
he if is really able to fail to buckle up only this once, then even
assuming independence above, 

P(ONE single auto trip in the United States resulting in a fatality) =
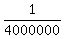 = 0.00000025 

and without independence it is an even smaller probability, and so he is 
willing to take that small risk.

Edwin