First you need to get both equations into Slope Intercept Form ( y = mx + b )
X + 2Y = 9 Subract X From Both sides
2Y = -X + 9 Divide Both Sides by 2
Y = -(1/2)X + 9 ( PURPLE LINE )
-X + 6Y = -1 Add X to both sides
6Y = X - 1 Divide both sides by 6
y = (1/6)X - (1/6)(GREEN LINE )
Now we have to graph these lines, see the graph below
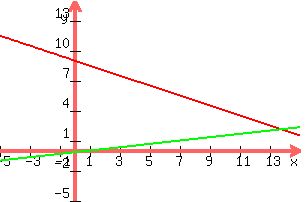
Now you have to estimate the intersection point... when you graph this on a calculator or a piece of graph paper you may get a more definitive answer, but for this exercise I am going to say those two lines intersect at (14,2)
Now do check them algebraically, you must take (14,2) and substitute 14 for X and 2 for Y, your goal is to get an equation that makes sense...
for example 2 = 2 makes sense because that is true, while 3 =2 does not make sense.
If you get an equation that makes sense, then the point we chose is the real intersection point, if the equation does not make sense, then we chose the wrong point.
Equation 1: Y = -(1/2)X + 9 Substitute ( 14, 2 ) into the equation
2 = -(1/2)*14 + 9 Simplfy
2 = -7 + 9 Add
2 = 2 ( check, this makes sense, so (14, 2) lies on the purple line )
You always need to check both equations just to make sure!
Equation 2: y = (1/6)X - (1/6)Substitue ( 14, 2 ) into the equation
2 = (1/6)*14 - (1/6) Multiply
2 = (14/6) - (1/6) Subtract
2 = 13/6 or 2(1/6)
Since this equation does not make sense, that means that ( 14, 2 ) is not the intersection, although it is close, it is not right on, so you would have you use your graph paper to make a better estimate.