|
Question 125252:
5) Find the equations of the horizontal and vertical asymptotes for the following. Type none if the function does not have an asymptote.
a) f (x)= 2x+3/x+2
Answer:
Horizontal:
Vertical:
b) g (x) = 5x/x^+1
Answer:
Horizontal:
Vertical:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
 Start with the given function Start with the given function
Looking at the numerator 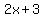 , we can see that the degree is , we can see that the degree is  since the highest exponent of the numerator is since the highest exponent of the numerator is  . For the denominator . For the denominator  , we can see that the degree is , we can see that the degree is  since the highest exponent of the denominator is since the highest exponent of the denominator is  . .
Horizontal Asymptote:
Since the degree of the numerator and the denominator are the same, we can find the horizontal asymptote using this procedure:
To find the horizontal aysmptote, first we need to find the leading coefficients of the numerator and the denominator.
Looking at the numerator 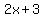 , the leading coefficient is , the leading coefficient is 
Looking at the denominator  , the leading coefficient is , the leading coefficient is 
So the horizontal aysmptote is the ratio of the leading coefficients. In other words, simply divide  by by  to get to get 
So the horizontal asymptote is 
--------------------------------------------------
Vertical Asymptote:
To find the vertical aysmptote, just set the denominator equal to zero and solve for x
 Set the denominator equal to zero Set the denominator equal to zero
 Subtract 2 from both sides Subtract 2 from both sides
 Combine like terms on the right side Combine like terms on the right side
So the vertical asymptote is 
Notice if we graph  , we can visually verify our answers: , we can visually verify our answers:
 Graph of Graph of  with the horizontal asymptote with the horizontal asymptote  (blue line) and the vertical asymptote (blue line) and the vertical asymptote  (green line) (green line)
b)
 Start with the given function Start with the given function
Looking at the numerator  , we can see that the degree is , we can see that the degree is  since the highest exponent of the numerator is since the highest exponent of the numerator is  . For the denominator . For the denominator 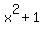 , we can see that the degree is , we can see that the degree is  since the highest exponent of the denominator is since the highest exponent of the denominator is  . .
Horizontal Asymptote:
Since the degree of the numerator (which is  ) is less than the degree of the denominator (which is ) is less than the degree of the denominator (which is  ), the horizontal asymptote is always ), the horizontal asymptote is always 
So the horizontal asymptote is 
--------------------------------------------------
Vertical Asymptote:
To find the vertical aysmptote, just set the denominator equal to zero and solve for x
 Set the denominator equal to zero Set the denominator equal to zero
 Subtract 1 from both sides Subtract 1 from both sides
 Combine like terms on the right side Combine like terms on the right side
 Take the square root of both sides Take the square root of both sides
Since you cannot take the square root of a negative number, the answer is not a real number. So in this case, there are no vertical asymptotes.
Notice if we graph  , we can visually verify our answers: , we can visually verify our answers:
 Graph of Graph of  with the horizontal asymptote with the horizontal asymptote  (blue line) . Notice how there are no vertical asymptotes (blue line) . Notice how there are no vertical asymptotes
|
|
|
| |