Question 124775: Write f(x) as a product of three linear factors
f(x)= x^3 -4x^2 -7x +10
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the cubic equation:  , the only possible rational roots are of the form x = factor of d/factor of a or x= -(factor of d/factor of a), so by trial and error find s such that , the only possible rational roots are of the form x = factor of d/factor of a or x= -(factor of d/factor of a), so by trial and error find s such that 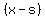 divides the original equation by polynomial long division without a remainder. divides the original equation by polynomial long division without a remainder.
For your problem, a = 1 and d = 10. The possible factors of d are 1, 2, and 5. 1 is the only factor of a. So if a rational root exists, it must be ±1, ±2, or ±5.
When I was working this out, I started with s = 1, dividing 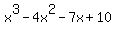 by by  . I got lucky, or so I thought. . I got lucky, or so I thought.
The quotient after performing the polynomial long division, was 
Now all that remains is to factor  . .  and and  , so our factors are , so our factors are 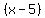 and and  . Turns out that luck wasn't a factor -- I had a 50-50 chance of finding the correct factor at the start, knowing that I had ±1, ±2, or ±5 to choose from. . Turns out that luck wasn't a factor -- I had a 50-50 chance of finding the correct factor at the start, knowing that I had ±1, ±2, or ±5 to choose from.
Therefore: 
I'll let you multiply it out to check the answer.
|
|
|