Read this lesson on completing the square by prince_abubu, if you do not know how to complete the square.
Let's convert  to standard form by dividing both sides by -3: to standard form by dividing both sides by -3:
We have:  .
What we want to do now is to change this equation to a complete square .
What we want to do now is to change this equation to a complete square  . How can we find out values of somenumber and othernumber that would make it work? . How can we find out values of somenumber and othernumber that would make it work?
Look at  : :  . Since the coefficient in our equation . Since the coefficient in our equation  that goes in front of x is -2.33333333333333, we know that -2.33333333333333=2*somenumber, or that goes in front of x is -2.33333333333333, we know that -2.33333333333333=2*somenumber, or  . So, we know that our equation can be rewritten as . So, we know that our equation can be rewritten as 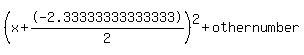 , and we do not yet know the other number. , and we do not yet know the other number.
We are almost there. Finding the other number is simply a matter of not making too many mistakes. We need to find 'other number' such that 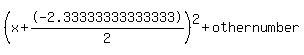 is equivalent to our original equation is equivalent to our original equation  . .

The highlighted red part must be equal to -1.66666666666667 (highlighted green part).
 , or , or  . .
So, the equation converts to  , or , or  . .
Our equation converted to a square 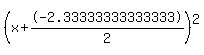 , equated to a number (3.02777777777778). , equated to a number (3.02777777777778).
Since the right part 3.02777777777778 is greater than zero, there are two solutions:

, or




Answer: x=2.90671775148509, -0.573384418151758.
|