|
Question 124605This question is from textbook Precalculus
: Can someone please help me a.s.a.p?
The solutions to ((1)/(x+2))-((2)/(x-1))>0
My answer options are:
a.(-infinity,5)U(1,infinity)
b.(-infinity,-5)U(-2,1)
c.(-5,-2)U(1,5)
d.(-2,1)U(5,infinity)
I thought the answer was b., what do you think? Thanks
This question is from textbook Precalculus
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Can someone please help me a.s.a.p?
The solutions to 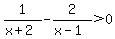 My answer options are:
a.(-infinity,5)U(1,infinity)
b.(-infinity,-5)U(-2,1)
c.(-5,-2)U(1,5)
d.(-2,1)U(5,infinity)
I thought the answer was b., what do you think? Thanks
My answer options are:
a.(-infinity,5)U(1,infinity)
b.(-infinity,-5)U(-2,1)
c.(-5,-2)U(1,5)
d.(-2,1)U(5,infinity)
I thought the answer was b., what do you think? Thanks
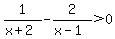 Get LCD on the left:
Get LCD on the left:
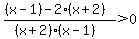
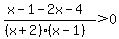
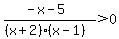 To find the critical values, set each factor
of the numerator and the denominator = 0, and
solve for x:
To find the critical values, set each factor
of the numerator and the denominator = 0, and
solve for x:
 yields critical value x = -5 yields critical value x = -5
 yields critical value x = -2 yields critical value x = -2
 yields critical value x = 1
Mark the critical values on a number line:
-------o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value left of -5, say -6.
Substitute it into: yields critical value x = 1
Mark the critical values on a number line:
-------o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value left of -5, say -6.
Substitute it into:
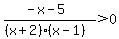
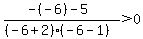
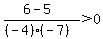
 That is true, so shade the part of the number
line to the left of -5.
<======o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Next, pick any value between of -5 and -2, say -3.
Substitute it into:
That is true, so shade the part of the number
line to the left of -5.
<======o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Next, pick any value between of -5 and -2, say -3.
Substitute it into:
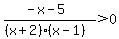
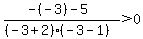
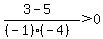
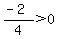
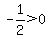 That is false, so do not shade the part of the number
line between -5 and -3, so we still have:
<======o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value between -2 and 1, say 0.
Substitute it into:
That is false, so do not shade the part of the number
line between -5 and -3, so we still have:
<======o--------o--------o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value between -2 and 1, say 0.
Substitute it into:
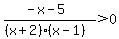
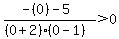

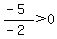
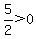 That is true, so shade the part of the number
line between -2 and 1.
<======o--------o========o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value right of 1, say 2.
Substitute it into:
That is true, so shade the part of the number
line between -2 and 1.
<======o--------o========o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Pick any value right of 1, say 2.
Substitute it into:
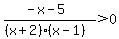

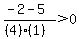
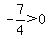 That is false, so do not shade the part of the number
line to the right of 1.
So far the number line so far gives:
<======o--------o========o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
We are technically supposed to test the critical values
themselves to see if they are solutions. But none do
since substituting -5 or -1 for x gives 0 > 0, and
substituting 1 for x causes the left side to be undefined.
So that number line is represented by this interval notation:
(-oo,-5) U (-2,1)
So you are correct since that's choice b.
Edwin
That is false, so do not shade the part of the number
line to the right of 1.
So far the number line so far gives:
<======o--------o========o------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
We are technically supposed to test the critical values
themselves to see if they are solutions. But none do
since substituting -5 or -1 for x gives 0 > 0, and
substituting 1 for x causes the left side to be undefined.
So that number line is represented by this interval notation:
(-oo,-5) U (-2,1)
So you are correct since that's choice b.
Edwin
|
|
|
| |