Discussion
Two variable systems of equations in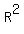 
come in two types:
1) Consistent: There is at least ordered pair in the solution set.
2) Inconsistent: The solution set is the empty set.
Consistent systems are further broken down into two types:
1) Independent: There is exactly one ordered pair in the solution set.
2) Dependent: There are an infinite number of ordered pairs in the solution
set
Graphically, this translates thusly:
If the lines have the same slope, they are either parallel or the same line.
Parallel lines represent inconsistent systems. Two equations that represent
the same line are a dependent consistent system.
If the lines have unequal slopes, they represent an independent consistent system.
Solution
Your first problem has two equations that are identical if you multiply the
first one by 3. That means that there are an infinite number of points that
will make either one of the equations a true statement -- you have an infinite
number of points in the solution, so you have a dependent consistent system.
Your second problem, if you put your equations into slope-intercept form by
solving each of them for y, you will note that the slope of one line is 1 and
the slope of the other is -1. Therefore, these lines intersect in exactly
one point and you have an independent consistent system.
In general if you have two equations in the form:
and
If 
then the system is consistent and dependent (same line,
infinite solutions)
If 
then the system is inconsistent (parallel lines, no
solution)
If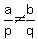 
then the system is consistent and independent (one solution)
