SOLUTION: Here is the problem The large rectangle shown is a gold rectangle. This means that when a square is cut off, the rectangle that remains is similar to the original rectabgle.

Algebra ->  Polygons -> SOLUTION: Here is the problem The large rectangle shown is a gold rectangle. This means that when a square is cut off, the rectangle that remains is similar to the original rectabgle.       Log On


   

Question 123994: Here is the problem
The large rectangle shown is a gold rectangle. This means that when a square is cut off, the rectangle that remains is similar to the original rectabgle.
The ratio of the length to width ina golden rectangle is called the golden ratio. Write the golden ratio in simplified radical form. Then use a calculator to find an approximation to the newest hundreth.
______________
|.....|........| (Ignore the periods in the rectangle. I had to do
|.....|........| that so it would look like a box.)
|.....|........| X
|.....|........|
|_____|________|
X
^------1-------^ < The measure of that whole bottom side is 1
So far I have concluded that x=1. As of what to do next I am completely on sure. My teacher gave me a hint to use the quadratic formula... but I still dont know what to do with it. Please help! THANK YOU!!!
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!





Discussion













To construct a golden rectangle, begin with a square (ABCD in the diagram) with

sides that measure 1 unit.



Extend one side of the square (red line in the diagram)





Bisect the side of the square that was extended (point E)





Strike an arc with radius DE to intersect the extended side of the square

(point F)





Construct the perpendicular to the extended side at F.





Extend the opposite side of the square to intersect the perpendicular at F.

(point G).





The resulting quadrilateral (ABFG) is a golden rectangle.





The dimensions of the golden rectangle are the measures of AB and BF.  But

BF = one half of BC plus EF.  But BC = AB, and EF = DE





The measure of DE can be determined by using the Pythagorean Theorem because

DE is the hypotenuse of a right triangle with sides CD measuring 1 and EC

measuring 1/2.







The rectangle that was added to the square is, itself, a golden rectangle

consisting of a square and a rectangle that is a golden rectangle, ad infinitum.










Solution







Let c = the measure of DE, a = the measure of EC, and b = the measure of CD.



a = 1

b = 1/2





c=sqrt%28a%5E2%2Bb%5E2%29





c=sqrt%28%281%29%5E2%2B%281%2F2%29%5E2%29





c=sqrt%285%2F4%29





c=sqrt%285%29%2F2





Since the measure of DE = the measure of EF and the measure of BE is 1/2,

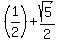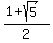
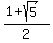the measure of BF (the length of the golden rectangle) is %281%2F2%29%2Bsqrt%285%29%2F2 or %281%2Bsqrt%285%29%29%2F2





%281%2Bsqrt%285%29%29%2F2 is roughly 1.62, so the Golden Ratio is approximately 1.62:1