|
Question 123847This question is from textbook
: How do I graph inequalities with two variable so that I will know what direction to shade solutions?
This question is from textbook
Found 4 solutions by rapaljer, solver91311, stanbon, MathLover1:
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! One way is to solve the equation for y (i.e., express the equations in slope-intercept form!).
If the inequality is written with a postive y coefficient and ">" or ">=", then you shade ABOVE THE LINE.
If the inequality can be written with a postive y coefficient and ">" or "<=", then you shade BELOW THE LINE.
For a more detailed explanation of this topic, see my website by clicking on my tutor name "rapaljer" anywhere in algebra.com. Then my first link of my home page is "Basic and Intermediate Algebra". Click on this, and go to Basic Algebra, Chapter 4, Section 4.04 Graphing Inequalities.
R^2
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Once you have graphed the line and decided whether it should be a solid line or a dashed line, pick a point on either side of the line. It doesn't matter where you pick the point, so choose something easy, like the origin (0,0). Substitute the coordinates of the chosen point back into the original inequality. If the result is a true statement, then you have chosen a point on the 'correct' side of the line -- shade in that side. If the result is a false statement, shade in the other side.
Example:
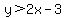 . Substitute (0,0): . Substitute (0,0): 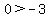 is a true statement, so the half-plane containing (0,0) is the solution set. is a true statement, so the half-plane containing (0,0) is the solution set.
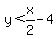 . Substitute (0,0): . Substitute (0,0): 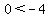 is a false statement, so the half-plane containing the origin is the 'wrong' side -- shade in the other side. is a false statement, so the half-plane containing the origin is the 'wrong' side -- shade in the other side.
Answer by stanbon(75887)   (Show Source): (Show Source):
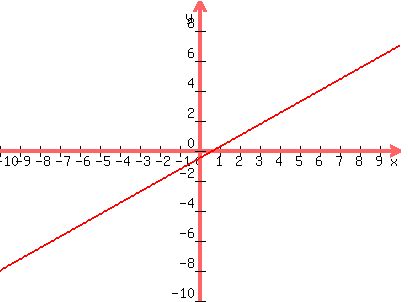
You can put this solution on YOUR website! Example:
3x - 4y < 2
1st: solve for "y":
y >= (3/4)x - (1/2)
---------------
2nd: Graph the boundary which is y = (3/4)x-(1/2)
Graph this line as a dashed line because "equality" was not part of the equation.
------------------------
3rd: Select a test point that is not on the boundary, like (0,0)
4th: Check to see if this point satisfied the INEQUALITY y>(3/4)x-(1/2)
You get: 0 > (3/4)*0-(1/2) ; 0>-1/2
----------------
Conclusion: That is true so the half-plane solution for the Inequality is on
the same side of the boundary as the point (0,0).
--------------
If the result had been false, the half-plane solution would be
on the side that does not contain (0,0)
=========================================
Cheers,
Stan H.
Answer by MathLover1(20850)   (Show Source): (Show Source):
|
|
|
| |