|
Question 123628: THIS IS AN ALGEBRA QUESTION FROM MY COLLEGE MATH CLASS THAT HAS ME TOTALLY CONFUSED, IF YOU CAN ANSWER THIS PLEASE DO SO AND SHOW HOW IT'S DONE.
THE QUESTION IS FIND A LINEAR EQUATION IN THE FORM OF P=MT+B(Y=MX+B)GIVING THE POPULATION (P) (t) years from 2010.now the numbers to substitute would be 6 years, and the set population is 2500 at an increase of 100 per year,please help if you can.thank you so very much
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! If I understand your problem correctly you are to find an equation in the form:
.

.
That will enable you to determine what the population will be some time in the future.
.
As you have recognized, this equation is in the slope-intercept form in which m is the slope
of the graph and B is the point where the graph intercepts the y-axis.
.
The letters above will represent the following quantities: P = population, m (the slope of
the graph) will represent the rate of change in the population, T will represent the number
of years that go by, and B is the known population at some point in time when T = 0.
.
You are told that the increase in population is 100 per year. That means that m equals 100.
Think of it this way ... how much will the population increase if 2 years go by? The answer
is 100 times 2 ... which is 100 times T. In 3 years the population would increase
by 100 times 3. It increases by m times T or 100*T and since T = 3 years, it goes up
by 100*3 or 300.
.
So now we can write the equation as:
.
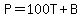
.
The problem then tells you that the base year is 2010. That is when T equals 0. If I interpret
your numbers correctly, in the year 2010 (when T = 0) the population will be 2500. If you
look at our equation and set T = 0, you get that P, the population, equals B. Since the
population is known to be 2500 at that time, the B must be 2500. Substituting this value
for B results in the equation becoming:
.

.
That should be the equation you are looking for. Just recognize that T is equal to the number
of years beyond 2010.
.
Using this equation you could now calculate the population in any year from 2010 on. For example,
in the year 2016 (which is 6 years after 2010 meaning that T = 6) the population would be
expected at:
.

.
So the population in 2016 could be expected to be 3100 persons.
.
Hopefully this answers your questions and if it doesn't at least it might give you enough insight
to see your way through to an answer.
|
|
|
| |