|
Question 123620: I am suppose to draw the graph of each line using its y-intercept and its slope..I have gone over the chapter and am just confused on how exactly i find that using this equation.  I am so ready to tear my hair out...can someone help?
thank you
Found 3 solutions by checkley71, stanbon, bucky:
Answer by checkley71(8403)   (Show Source):
You can put this solution on YOUR website! THE STANDARD LINE FORMULA IS:
Y=mX+b WHERE m=THE SLOPE & b=Y INTERCEPT.
NOW CONVERT YOUR EQUATION TO THIS FORM THUS:
4X+3Y=9
3Y=-4X+9
Y=-4X/3+9/3
Y=-4X/3+3 ANSWER
THIS REPRESENTS A LINE WITH A SLOPE OF -4/3 & THE Y INTERCEPT IS 3.
 (graph 300x300 pixels, x from -5 to 5, y from -5 to 5, y = -4x/3 +3).
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website! 4x+3y=9
------------
Solve for y : 3y=-4x+9
y = (-4/3)x+3
-----------------
The y-intercept is the point (0,3)
The slope is -4/3
-----------------
slope means "change in y"/"change in x"
Your change in x is +3;
Your change in y is -4
--------------------------
Put your pencil point on the y-intercept: put a dot there.
Move your pencil point +3 to the right, then 4 down; to the
point (3,-1); put a dot there.
Now draw a line thru the two points. That is the graph you want.
=================
Cheers,
Stan H.
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! One way to do this problem is to rearrange the given equation into the slope-intercept
form. The slope-intercept form of an equation is:
.
.
in which m, the multiplier of the x, will be the slope and b, a constant, is the value on
the y-axis where the graph intercepts (crosses) the y-axis.
.
For this problem you were given the equation:
.
.
To get this equation into the slope-intercept form, let's solve it for y.
.
Begin by getting rid of the 4x term on the left side, so that only the term containing y
remains on the left side. You can do this by subtracting 4x from both sides. When you
subtract 4x from the left side the 4x on the left side goes away. And when you subtract 4x
from the right side you get a -4x on the right side. This means your equation has become:
.
.
Then to solve for y, you just divide both sides of the equation by 3. On the left side
dividing 3y by 3 results in the left side becoming just y. And on the right side you divide
both terms by 3. This division makes the equation become:
.
.
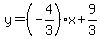
Finally recognize that the 9 divided by 3 on the right side is just 3. Therefore, the
equation finally becomes:
.
.
Note that this equation is in the slope-intercept form. The left side is just y. On the right
side the multiplier of the x is 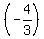 and that is the slope. And the constant term
of +3 is the value on the y-axis that the graph crosses through.
.
One thing you can immediately tell is that the slope is negative which means that in going
from the left to the right the graph slopes down. And since the slope is defined as the
change in the value of y divided by the change in the value of x, from the fraction
-4 divided by 3 that y will go down 4 units for every 3 units that x goes to the right. You
already know that the point +3 on the y-axis (the point (0, +3) is on the graph. Put your
pencil on that point. Then move your pencil horizontally to the right 3 units. At that point
go vertically down 4 units. Stop there and make a mark. That is a second point on the graph.
[You should be at the point (3, -1)]. You can now extend a straight line through the two points.
That line will be the graph you are looking for.
.
At this point you should have a graph that looks like this:
.
.
Hope this helps you to see how to convert equations to slope-intercept form and how to
make a graph once you have the equation in slope intercept form.
.
A couple of final comments. If your slope intercept equation has an integer (whole number)
as the multiplier of x, when you think of the slope put that integer over 1.
.
For example, suppose the slope intercept form of the equation was:
.
.
(I just made this up as an example. It has nothing to do with the problem you were given
to work.)
.
You would know that the graph crosses the y-axis at -7. And you would also know that the
slope is +3/1 ... meaning that for every horizontal change of 1 unit to the right, the graph
would go vertically up 3 units. For this made up example the graph would look like this:
.
|
|
|
| |
