SOLUTION: your class is building a diorama of the National Mall in Washington, DC using scale 1 in. = 1.5 ft. On the mall the distance between Washington Monument and the Lincoln Memor

Click here to see ALL problems on Geometric formulas

Question 123278: your class is building a diorama of the National Mall in Washington, DC using scale 1 in. = 1.5 ft.

On the mall the distance between Washington Monument and the Lincoln Memorial is approximately 3/4 mile. What distance should you use in your diorama??
how would i solve this with out it confusing me cause i don't get math and it's confusing!

Found 2 solutions by solver91311, bucky:
Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!
If 1 inch in the model equals 1.5 feet in real life, then 1 inch in the model equals 18 inches in real life . That means the scale is 1:18.

There are 5280 feet in 1 mile, so 3/4 of a mile is feet.

Now, since the scale is 1:18, every 18 feet in real life is represented by 1 foot in the model. So the question becomes how many 18s are in 3960?

feet.

So 3/4 mile would be represented by 220 feet in the diorama model.

Now you really have a problem! Since the Washington is in the middle of the National Mall, that 220 feet is only 1/2 of the length of your entire diorama. The whole thing would have to be 440 feet long or just under 150 yards. You need a one and a half football fields to build this thing at this scale. You would do better to have a scale of 1 inch = 150 feet. That gets your model down to a much more manageable 4.4 feet long.

Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website!
Let's first just think our way through this problem without worrying about remembering an
equation from a book.
.
Your problem tells you that you are going to use a scale of 1 inch equals 1.5 feet for your model.
This means that if a distance in the real world is 1.5 feet, then in your model that distance will
be 1 inch. So if you have a distance or length of 3 feet in the real world, your model will have
that distance as 2 inches ... because each of those inches represents 1.5 feet so 2 inches represents
2 times 1.5 feet or 3 feet. In the real world a person is 6 feet tall. How tall is that in the
model? The answer is that 1 inch equals 1.5 real world feet, 2 inches is 3 real world feet, 3 inches
is 1.5 + 1.5 + 1.5 or 4.5 feet. And finally 4 inches is 1.5 + 1.5 + 1.5 + 1.5 feet or a total
of six feet. So a model of a 6 foot tall person would be 4 inches tall.
.
Using this same method, if we divide the real world length by 1.5 feet, the answer will be
the number of inches the length will be in the model.
.
In our example of a 6-foot tall person, 1.5 goes into 6 four times. And for each of those four units
of 1.5 feet, the corresponding height of the model is 1 inch. So 4 units of 1.5 feet requires
4 inches in the model.
.
Similarly, a real world length of 90 feet will be 90/1.5 = 60 inches. And a real world length of
150 feet will be 100 inches long in the model because there are a hundred 1.5 ft units in 150 feet.
.
Your problem wants to know how long a real world distance of 3/4 of a mile would be in your model.
.
First, we need to know how many feet are in 3/4 of a mile. A mile is 5280 feet and 3/4 of a mile
is 3/4 of 5280 feet. You can find this by multiplying 5280 times 3 and dividing that answer
by 4. Or another way to do it would be to multiply 5280 by 0.75 because 0.75 is equivalent to
three-quarters. Anyhow, what ever way you choose to do this you should find that there are 3960 feet in
three-quarters of a mile. Then if you divide 3960 by 1.5 you find that the answer is 2640.
This tells you that three-quarters of a mile in the real world will be represented by
2640 inches in your model. And since 12 inches are equal to a foot, if we divide 2640 inches by 12
you will find that the quotient is 220. This tells you that 2640 inches equals 220 feet. So three-quarters
of a real world mile will be 2640 inches or 220 feet in your model.
.
With that as a background, let's discuss how you might use a proportion to solve this problem.
.
The ratio of your model distance to the real life distance is:
.

.
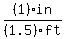
And this will be x inches of model distance divided by real life distance (d) in feet. So
we can write the proportion:
.

.
Notice that in each side of this proportion the numerators are the model length in inches and
the denominators are the real world length in feet.
.
We need to get d in feet just as we did above ... by finding three-quarters of 5280 feet. The answer
to that is 3960 feet. Substitute that for d in the proportion and you have:
.

.
You can solve this by cross-multiplying ... which is multiplying the numerator on one side
by the denominator on the other side ... and doing that for both numerators. Then set the two
products equal. In this case you would multiply the numerator 1 times the denominator 3960 to
get the product of 3960. Then you would multiply the numerator x by the denominator 1.5 to
get a product of 1.5x. You set these two products equal and you have:
.

.
and you solve for x by dividing both sides of this equation by 1.5 to get:
.

.
So the length in the model is 2640 inches ... the same as we got previously. And if you divide this
answer by 12 inches per foot you find that the length in the model is 220 feet.
.
Hope this helps you to see how this problem works.
.